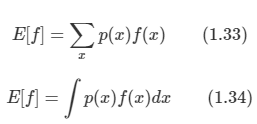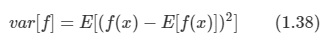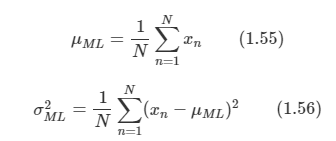*Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

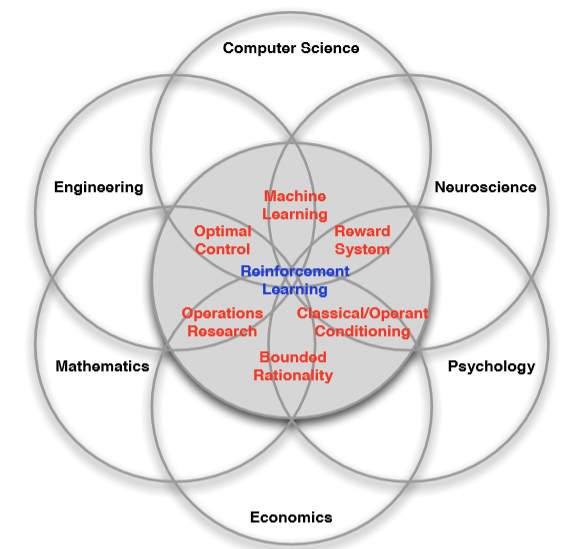
강화학습은 여러 분야에서 사용가능하다. 컴퓨터 과학, 공학, 수학, 경제학 등 여러 분야에서 사용 가능하다.

• 머신러닝은 지도 학습, 비지도 학습, 강화 학습 세 분야로 나눌 수 있는데, 강화 학습에 대해 자세히 알아보도록 한다.

• 강화학습이 다른 머신러닝 분야들과 다른점은 무엇일까?

  • supervisor가 존재 하지 않는다.(y 값이 존재하지 않는다.) 대신 reward라는 값이 존재한다.
  • Feedback을 바로 받는 것이 아니라 일련의 행동들이 모두 마친 뒤에 나타난다.
  • 내가 이전에 한 행동에 따라 결과가 바뀌게 된다. 즉 시점에 따라 행동이 다르다.
  • agent의 행동에 따라 얻는 데이터가 달라지게 된다. (agent는 뒤에 다시 소개한다.)

• 강의에서 다음과 같은 예시들을 소개하고 있다.

  • Fly stunt manoeuvres in a helicopter(자율주행)
  • Defeat the world champion at Backgammon(유럽의 보드게임)
  • Manage an investment portfolio(주식)
  • Control a power station(발전소 관리)
  • Make a humanoid robot walk(로봇이 걷도록 하는것)
  • Play many different Atari games better than humans(알파고(Atari 게임))

• Reward (Rt)

  • scalar 피드백 값, 얼마나 agent가 t 단계에서 잘 수행했는지를 나타낸다.
  • agent의 임무는 누적 보상을 최대화 하는 것.
  • 강화 학습은 reward hypothesis에 기반을 두고 있다.
    • reward hypothesis?
      • 기대 누적 보상을 최대화하는 것이 agent의 목표이다.

• Sequential Decision Making

  • Goal : 총 reward를 최대화 하는 행동을 고르는 것.
  • 행동은 긴 기간 동안 연속적으로 발생하며 보상은 이 행동들이 마친 뒤에 얻게 된다.
  • 이로써 나중에 더 큰 보상을 얻을 수 있다면 지금 당장은 적은 보상을 선택하거나 손해를 볼 수도 있음을 의미한다.

Agent and Environment

• agent
  • environment의 observation, reward를 받아서 agent가 action을 수행한다.
• Environment
  • agent의 action을 받아서 바뀐 observation, reward를 agent에 전달해준다.

즉 agent는 사람, envionment는 지구로써 사람이 어떤 행위를 취하면 지구에 영향을 주게 되고 지구의 환경에 변하며 이는 다시 사람에게 영향을 주게 된다.(지구 온난화?)

History and State

• history는 observation, actions, rewards를 일련적으로 표현한 것.

• state는 다음에 어떤 것을 해야 하는지 결정에 도움을 주는 정보, 이 것은 history에 특정한 함수를 취함으로써 얻는다.

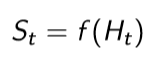
Environment state and Agent State

agent, environment가 각각 가지고 있는 상태, 정의상으로는 agent state는 알고 있지만 envionment state는 모른다.( ex) 사람은 자신의 정보를 바탕으로 행동을 하지만, 그렇다고 지구의 환경이 어떻게 변할지는 예측할 수 없다.(또는 매우 힘들다)

Markov state(information state)

'Markov하다' 라는 정의로 미래는 과거에 어떤 상태였는지는 관계 없이 현재 상태만이 영향을 준다는 것이다. 다음 강의에서 Markov에 대해서 자세히 설명하기 때문에 이번엔 정의만 보고 넘어간다.

• Full observability : agent가 agent state, environment state를 모두 아는 것, 이러한 경우에 Markov decision Process라고 부르며 다음 강의에서 자세히 다룬다.

RL's major components

• Policy
  • agent의 행동을 의미한다. 어떤 현재 상태에 있을 때 어떠한 행동을 할지를 나타낸다.
  • 결정론적 정책
    • 상태 s에 도달하면 항상 a라는 행동을 한다.
  • 통계학적 정책
    • 상태 s에 있을 때 일정한 확률에 따라 특정한 행동 a를 한다.
• Value Function
  • 미래 reward의 예측을 하는데 사용한다.
  • 이 값으로 상태가 좋은지/나쁜지 판단할 수 있다.
• Model
  • 환경에 다음에 어떠한 것을 할 지 예측하는 것
  • 즉 다음에 어떤 상태가 발생되고, reward가 발생하는지 알려준다.

Categorizing RL agent

• Value Based
  • Value Function
• Policy Based
  • Policy
• Actor Critic
  • Policy
  • Value Function
• Model Free
  • Policy and Value Function
• Model Based
  • Policy and Value Function
  • Model

Learning and Planning

• Reinforcement Learning
  • 환경은 초기에 알려져 있지 않다.
  • agent는 환경과 상호작용한다.
  • agent는 정책을 발전시킨다.
• Planning
  • 환경의 모델을 알고 있다.
  • agent는 그 모델에서 계산을 수행한다.
  • agent는 정책을 발전 시킨다.

Exploration and Exploitation

• Exploration(탐험)
  • 탐험은 전체 공간을 골고루 찾아보는 전략이며 항상 같은 방향으로 진행하지 않는다.
• Exploitation(탐사)
  • 탐사는 특정한 곳 주위를 집중적으로 찾아보는 전략으로 보상이 최대화 되는 방향으로만 진행한다.
• 이들은 trade-off 관계에 있으며, 탐험은 시간이 너무 오래 걸리고, 탐사는 지역 최적해에 머무는 문제가 발생한다.

https://www.youtube.com/watch?v=2pWv7GOvuf0&list=PLqYmG7hTraZDM-OYHWgPebj2MfCFzFObQ

강화학습으로 가장 유명한 알파고가 있으며 알파고를 만든 회사인 deepmind에서 David Silver가 강화학습에 대해 강의한 자료를 제공하고 있다. 따라서 이 강의를 보면서 정리한 내용들을 앞으로 올려보도록 한다.

https://www.youtube.com/watch?v=2pWv7GOvuf0&list=PLqYmG7hTraZDM-OYHWgPebj2MfCFzFObQ

아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.

1. 소개(Introduction)

• 패턴인식이란 컴퓨터 알고리즘을 활용하여 데이터의 규칙성을 자동적으로 찾아내고, 이 규칙성을 이용하여 데이터를 각각의 카테고리로 분류하는 등의 일을 하는 분야

• 휴리스틱 알고리즘을 통해 생성된 규칙으로 문제를 해결할 수 있다.

  • 각각의 규칙에 대해 예외 사항을 적용해야 하며 이로 인해 수많은 rule을 만들어야 함.

  

• 머신러닝을 사용하면 더 나은 결과를 얻을 수 있다. 위와 같이 손으로 쓴 숫자를 분류하는 예제가 있다고 하자. 그러면 N개의 숫자들을 training set으로 활용하고, 각 숫자의 카테고리를 표적 벡터로 표현해 매개변수를 조절해 학습한다.

일반화(Generalization)

• 훈련 데이터가 실제 모든 데이터를 대변하지 많는다.

• 따라서 가지고 있는 데이터를 통해 새로운 예시들을 올바르게 분류하는 능력을 일반화(Generalization)이라고 한다. 이는 패턴 인식의 가장 중요한 목표다.

• 입력 데이터를 사전에 정제하는 작업을 진행하는데 이 과정을 통해 문제를 더 쉽게 해결할 수 있다.
  • 이 과정을 전처리(preprocessing) 또는 특징 추출(feature extraction) 과정이라고 부른다.

기계 학습의 종류

• 지도 학습(Supervised Learning)

  • 주어진 훈련 데이터가 입력 벡터와 그에 해당하는 표적 벡터로 이루어지는 문제
  • 분류(classification), 회귀(regression)

• 비지도 학습(Unsupervised Learning)

  • 훈련 데이터가 해당 표적 없이 오직 입력 벡터 x로만 주어지는 경우
  • 군집화(clustering), 밀도 추정(density estimation)

• 강화 학습(Reinforcement Learning)

  • 주어진 상황에서 보상을 최대화하기 위한 행동

  • 지도학습과는 다르게 입력값과 최적의 출력 값을 예시로 주지 않음

  • 탐험(Exploration)과 탐사(Exploitation) 간의 트레이드오프 문제

1.1 Example

 실숫값의 입력 변수인 x를 관찰한 후 이 값을 바탕으로 실숫값의 타깃 변수인 t를 예측하려 한다.

• 예제에 사용될 변수를 가정하자.
  • N개의 관찰값 x로 이루어진 훈련 집합 x=(x1, x2,... xN)^T, 타깃 변수 t=(t1,..., tN)^T
  • tn은 sin(2 pi x)의 출력값에 가우시안 분포만큼의 노이즈를 더해서 만들었음

• 그림에서 녹색 선이 sin(2 pix) 함수이며, 파란색 원이 가우시안 랜덤 분포에 의해 발생한 샘플

  • 관측된 값들은 노이즈로 인해 변질되어 있어서 각각의 주어진 x에 대해서 어떤 값이 적합한 t인지가 불확실하다.
  • 1.2절에서 진행할 확률론에서 더 자세히 이야기할 것이다.

• 해당 곡선을 fitting 하기 위해서 다음과 같은 형태의 다항식을 활용한다.

  

  • 다항식을 사용한 이유는 추후에 설명하도록 한다.

• 훈련 집합의 표적 값들의 값과 함숫값 y(x, w)와의 오차를 측정하는 오차 함수(error function)를 정의하고 이 함수의 값을 최소화하는 방식으로 피팅할 수 있다.

  

  • 위와 같이 오차 함수를 사용하며 각각의 데이터 포인트에 대한 예측치와 해당 표적값 사이의 오차를 제곱하여 합산하는 방식이다. 그리고 1/2는 나중의 편의를 위해서 추가되었다.

• 우리는 E(w)를 최소화하는 w 값을 선택함으로써 이 곡선 피팅 문제를 해결할 수 있다.

  • 오차 함수가 이차 다항식의 형태를 지니고 있기 때문에 이 함수를 계수에 대해 미분하면 w에 대해 선형인 식이 나올 것이고, 오차 함수를 최소화하는 유일한 해를 찾아낼 수 있을 것이다.
  • 유일한 해 w를 앞으로 w*라고 표현한다.

• 다항식의 차수 M을 결정해야 한다.

  • 이 문제를 Model comparison(모델 비교), Model Selection(모델 결정)이라 부른다.
  • 차수 M에 따라서 표현되는 곡선이 달라지므로 어떠한 차수를 선택할지는 중요하다.

• M = 0,1,3,9 인 경우에 대해 다항식으로 피팅하는 예시다.

  

  • M=0 ,1 인 경우에는 함수를 잘 표현하지 못하는 것으로 보인다.
  • M=3 인 경우에는 가장 잘 표현하는 것으로 보인다.
  • M=9 일 경우에 완벽하게 피팅이 되는 경우로 오차 함수의 값이 0일 것이다.
  • 하지만 M=3 인 경우를 선택하는 것이 가장 좋은 선택이다.
    • 최종 목적은 새로운 데이터 x가 입력되는 경우에 가장 적합한 결과를 제공하는 일반화 모델을 얻는 것이다.
    • M= 9인 경우에는 새로운 데이터에 대해 매우 좋지 못한 성능을 보일 것이다.

• 이처럼 주어진 데이터에 비해 M이 너무 클 경우를 과적합(over-fitting)이라고 하고, 너무 작을 경우를 과소 적합(under-fitting)이라고 한다.

  • 과적합은 bias가 작고, variance가 크다고 하며, 과소 적합은 bias가 크지만 variance가 작다고 한다.
  • bias와 variance는 트레이드 오프 관계이다.

• 일반화의 성능을 측정할 수 있는 수치가 있으면 편리하다. 따라서 RMS 에러(Root Mean Square error)를 사용한다.

  

  • N으로 나눔으로써 데이터 사이즈가 다른 경우에도 비교할 수 있도록 했고, 제곱근을 취함으로 표적 값과 같은 크기를 가지도록 했다.
  • RMS가 작을수록 더 좋은 모델임을 의미한다.

  

• 각각의 M에 대해서 RMS의 값을 확인해보면 과적합 되는 지점을 알 수 있다.

  • RMS의 값이 M이 커질수록 작아지는 것은 당연하다.
  • 대신 M=9처럼 test의 RMS가 급격하게 커지는 구간을 과적합 되는 지점이라고 할 수 있다.

• 데이터의 크기에 따라 모델의 결과가 달라진다.

  

  

  • 위 그림에서 사용한 M의 값은 9로 동일하며 왼쪽은 N=15, 오른쪽은 N=100의 샘플 크기가 존재한다.
  • M=9를 사용했지만 N=100일 경우 과적합의 흔적이 보이지 않는다.
    • 즉 과적합 문제는 더 많은 샘플을 확보함으로써 해결할 수 있다.
  • 앞으로 최대 가능도(Maximum likelihood), 베이지안(Bayesian) 방법을 사용해 과적합 문제를 해결할 수 있다.

• 정규화(regularization)를 통해 제한적인 양의 데이터 집합을 통해 복잡하고 유연한 모델을 생성할 수 있다.

  • 과적합이 발생한다면 w의 값이 매우 커지거나 매우 작아지는 현상이 발생한다. 따라서 이를 막기 위해 패널티 항을 추가하는 방식이다.

  

  • 여기서 ||w||^2 = W^TW 이며, 계수 람다가 정규화항의 제곱합 오류항에 대한 상대적인 중요도를 결정짓는다.

• 람다에 대해서 더 알아보도록 한다.

  

  

  • 그림을 통해 M=9이고 동일한 크기의 샘플 데이터가 적용된 결과에 람다를 추가하면 위와 같은 현상이 발생한다.
  • ln 람다 = -18인 경우 과적합이 없어지고 원래 근사하려던 식과 매우 유사해진다.
  • 하지만 ln 람다 = 0을 보면 지나치게 큰 람다는 과소적합 현상을 만들어낸다.

1.2 확률론

패턴 인식 분야에서 중요한 것 중 하나는 ''불확실성''이다. 불확실성은 노이즈를 통해서도 발생하고 데이터 집합의 수가 제한되어 있어서 발생하게 된다.

• 확률론(Probability Theory)

  • 불확실성을 계량화하고 조작하기 위한 이론적인 토대를 마련해 주며, 패턴 인식 분야의 중요한 기반

  

• 위 그림의 예시를 통해서 확률론에 대해서 알아보도록 하자.

  • 두 개의 상자가 주어지고, 하나는 빨간색 상자, 다른 하나는 파란색 상자라고 하자.
  • 빨간색 상자에는 6개의 오렌지, 2개의 사과가 있다.
  • 파란색 상자에는 1개의 오렌지, 3개의 사과가 있다.
  • 랜덤하게 상자 하나를 골라 임의로 과일 하나를 꺼내고 넣는 작업을 수행하며, 상자 안에서 각각의 과일을 고를 확률을 동일하다.
  • 빨간색 상자를 고를 확률은 0.4, 파란색 상자를 고를 확률은 0.6이라고 하자.
    • p(B=r) = 4/10, p(B=b) = 6/10
  • 이제 '사과를 고를 전반적인 확률은?', '오렌지를 선택했을 때 파란 상자였을 확률은?'과 같은 질문에 답할 수 있어야 한다.

• 이를 위해 확률의 두 가지 기본 법칙은 합의 법칙(sum rule), 곱의 법칙(product rule)에 대해서 알아본다.

  • 합의 법칙

    

  • 곱의 법칙

    

  • 위 수식들은 다음과 같은 과정을 통해 얻을 수 있다.

    

    

    • X가 xi, Y가 yj 일 확률을 위와 같이 적는다. 이때 Y 값과 무관하게 X가 xi 값을 가질 확률을 구해보자.

      

    • 이 때 ci = 시그마 nij이다. 이로부터 합의 법칙을 유도할 수 있다.

      

    • 곱의 법칙도 비슷하다.

      

    • 1.8의 식을 X=xi일 때, Y=yj일 경우를 의미하며 이를 조건부 확률이라고 한다. 따라서 1.5,1.6,1.8을 통해서 다음 1.9와 같은 관계를 도출할 수 있으며 이것이 바로 곱의 법칙이다.

• 합의 법칙과 곱의 법칙을 이용하여 베이즈 정리를 기술할 수 있다.(유명한 정리이므로 자세한 설명은 생략한다.)

  

  • 이것을 토대로 사과와 오렌지 예제에 적용하면 다음과 같다.

  

1.2.1 확률 밀도(probability density)

• 지금까지는 이산적인 사건을 바탕으로 확률에 대해 알아보았다면 이번에는 연속적인 변수에서의 확률에 대해 알아보도록 한다.

  

  • 위와 같이 표현되는 것을 확률 밀도(probability density)라고 부른다.

  • 확률은 양의 값을 가지고 x의 값은 실수에 존재해야 한다. 따라서 확률 밀도 함수는 아래 두 조건을 만족시켜야 한다.

    

  • x에 대해 확률 함수 p(x)가 주어졌을 때 구간 (-무한, z)에 대한 확률 값을 누적 분포 함수(cumulative distribution function)라고 한다.

    

  • 위 그림을 보면 이해하기 쉬우며, P(x)를 미분하면 p(x)를 얻을 수 있다.

1.2.2 기댓값과 공분산(Expectation and covariance)

• 확률식에서 주어진 데이터에 대한 무게 중심을 구하는 것은 매우 중요한데, 주로 평균(기댓값)이 사용된다.

  

  • 이산 분포, 연속 분포에 일 때의 기댓값을 구하는 방법이다.

  • 간혹 여러 개의 변수를 사용하는 함수에 대해 평균값을 표기할 경우가 있다,

    • 이 때는 평균에 사용하는 주변수에 대해 기술한다.

      

    • f(x, y)의 평균값을 x의 분호에 대해 구하라는 의미이다.

• f(x)의 분산은 다음과 같이 정의된다.

  

  • 분산은 f(x)가 평균값 E [f(x)]로부터 전반적으로 얼마나 멀리 분포되어 있는지를 나타내는 값이다. 위 식을 전개하면 f(x)와 f(x)^2의 기댓값으로 표현할 수도 있다.

    

  • 2개의 랜덤 변수 x와 y에 대해 공분산은 다음과 같이 정의된다.

    

  • x와 y가 서로 독립이라면 공분산 값은 0이 된다.

1.2.3 베이지안 확률

• 지금까지 확률을 ''반복 가능한 임의의 사건의 빈도수''라는 측면에서 봄. 이러한 해석을 고전적 혹은 빈도적이라고 한다.

• 베이지안 관점을 사용하면 확률을 이용해서 불확실성을 정량화하는 것이 가능하다.

  • 베이지안 관점은 확률의 개념을 빈도가 아닌 믿음의 정도로 고려하는 것

• 앞에서 말했던 예제인 곡선 피팅 문제를 다시 생각해보자. 이 문제에서 w가 알려지지 않은 고정된 값으로 여겨졌는데 베이지안 관점을 적용하면 w에 대한 불확실성을 기술할 수 있다.

  

  • 이 식은 관측하기 전의 w에 대한 가정을 p(w)로 표현을 하고 w의 불확실한 정도를 수식에 반영하고 있다.

    • p(w)는 모수에 대한 사전 확률 분포를 의미

    • p(w|D)는 D를 관측한 후의 w에 대한 불확실성을 사후 확률로 표현

    • p(D|w)는 가능도 함수(likelihood function)이라고 불리며, 각각의 다른 매개변수 벡터 w에 대해 관측된 데이터 집합이 얼마나 '그렇게 나타날 가능성이 있었는지'를 표현

    • 최종적으로 다음과 같은 식을 만들 수 있다.

      

    • 식 1.43의 양쪽 변을 w에 대해 적분하면 베이지안 정리의 분모를 사전 확률과 가능도 함수로 표현할 수 있다.

      

• 더 자세한 내용은 2장에서 살펴보도록 한다.

1.2.4 가우시안 분포

2장에서 다양한 확률 분포와 각각의 성질에 대해 살펴볼 것인데, 가우시안 분포에 대해 간단히 개념을 살펴보고 간다.

• 가우시안 분포는 두 개의 매개변수 u와 시그마^2에 의해 통제된다. u는 평균, 시그마^2은 분산이며, 분산의 제곱근 값은 표준 편차라 불린다. 또한 분산의 역에 해당하는 값은 정밀도라고 한다.

  

  

• 가우시안 분포를 정규 분포라고도 부르며 다음과 같은 성질들이 있다.

  

• 모든 값에서 0보다 큰 값을 가지고 전체 합은 1이라는 특징은 정규화의 특징으로써 가우시안 분포가 정규화되어 있음을 알 수 있다.

  

  • 가우시안 분포의 기댓값과 분산은 위와 같다.

• 하나의 관찰 데이터 집합 x=(x1, x2, x3,..., xN) T이 주어졌다고 하자. 그러면 데이터 집합 하나가 관찰될 수 있는 확률은 얼마일까?

• 같은 분포에서 독립적으로 추출된 데이터 포인트들을 독립적이고 동일하게 분포(i.i.d) 되었다고 한다.

  • 따라서 각 사건의 주변 확률의 곱으로 표현이 된다. 따라서 조건부 확률로 다음과 같이 적을 수 있다.

    

  • 이것을 그림으로 나타내면 다음과 같다.

    

  ---

• 실제로 얻는 것은 관찰 데이터 집합이고 이를 이용하여 원래의 가우시안 분포를 결정하는 문제를 풀어야 한다.

  • 즉 주어진 샘플이 어떠한 특징을 가지고 있는 가우시안 분포에서 나왔는지를 찾으라는 이야기이며, 평균과 분산의 값을 구하면 된다.

  • 따라서 식 (1.53)의 가능도 함수를 최대화하는 방식으로 평균과 분산을 찾으면 된다.

  • 로그 함수는 변수에 대해 단조 증가하는 함수이므로 로그를 취한 후 최댓값을 찾을 수 있다. 이 점이 분석이 간단해지고 수치적인 측면에서도 도움이 되기 때문이다.

    

• 이 함수의 해는 다음과 같다. 각각의 표본 평균, 표본 분산이라고 부른다.

  

1.2.5 곡선 피팅

• 이전에는 다항식 곡선 피팅 문제를 오차 최소화 측면에서 살펴보았는데, 이번에는 확률적 측면에서 살펴본다.

  • 이를 통해 오차 함수와 정규화에 대한 통찰을 얻을 수 있다.
  • 베이지안 해결법을 도출하는데 도움이 될 것이다.

• 곡선 피팅 문제의 목표는 가지고 있는 샘플 데이터들로 새로운 입력 변수가 주어졌을 때 그에 대한 타깃 변수를 예측해 내는 것이다.

  • 따라서 확률 분포를 이용해 타깃 변수의 값에 대한 불확실성을 표현할 수 있다. 노이즈를 가우시안 분포로 고려하면 다음과 같이 표현할 수 있다.

    

  • B는 정밀도 매개변수를 의미한다. 이를 그림으로 표현하면 아래와 같다.

    

  • 즉 한 점이 주어지고 그 점을 중심으로 가우시안 노이즈가 존재하는 것과 같다.

• 훈련 집합을 바탕으로 최대 가능도 방법을 이용하여 파라미터들을 결정할 수 있다. 가능도 함수는 다음과 같다.

  

• 로그를 취하고 이 가능도 함수를 최대로 만드는 파라미터 값을 추정한다.

  

• MLE를 이용해 얻어진 해 w를 wML로 표기를 하며 마지막 두 term은 w에 관계없으니, 제거, 계수의 B/2도 1/2로 바꿀 수 있다. 마지막으로 로그 가능도를 최대화하는 대신에 로그 가능도의 음의 값을 취한 후, 이를 최소화하면 제곱항 오차 함수를 유도할 수 있게 된다.

  

• 위와 같은 방식으로 새로운 데이터의 타겟 값을 예측할 수 있으며 이를 예측 분포라고 한다.

  

  • 베이지안 방식을 위해 다항 계수 w에 대한 사전 분포를 도입한다.

    

  • 여기서 a는 분포의 정밀도이며, M+1은 M차수 다항식 벡터 w의 원소의 개수다. a와 같이 모델 매개변수의 분포를 제어하는 변수들을 하이퍼 파라미터(hyperparameter)라고 한다.

  • 베이즈 정리를 이용하면 다음과 같이 식을 쓸 수 있다.

    

  • 이제 주어진 데이터에 대해 가장 가능성 높은 w를 찾는 방식으로 w를 결정할 수 있다. 즉, 사후 분포를 최대화하는 방식으로 w를 결정할 수 있다. 이 방식을 최대 사후 분포(MAP maximum posterior)라 한다.

    

1.2.6 베이지안 커브 피팅

• 아직 w에 대해 점 추정을 하고 있기 때문에 아직은 완벽한 베이지안 방법론을 구사한다고 말할 수 없다. 완전한 베이지안적 접근을 위해 모든 w에 대한 값을 반영해야 한다. 따라서 모든 w에 대해 적분을 시행하게 된다.

  

• 적분을 시행하면 다음과 같이 가우시안 분포로 주어진다.

  

• 여기서 평균은 다음과 같다.

  

1.3 모델 선택

• 지금까지 최소 제곱법을 이용하여 곡선 피팅의 예시에서 최적의 다항식 차수가 있음을 알 수 있었다.

  • 다항식의 차수에 따라 자유 매개변수의 수가 결정되며, 모델의 복잡도가 결정되었다.
  • 정규화 계수도 복잡도에 영향을 주었다.
  • 실제 응용 사례에서는 이러한 매개변수의 값을 결정해야 하며, 가장 적합한 모델을 선택해야 한다.

• 대부분의 경우에는 train과 test에 대한 데이터의 공급이 제한적이다. 이런 상황에서 해결할 수 있는 한 가지 방법이 교차 검증법 (cross-validation)이다.

  • 임의로 고른 (S-1)/S를 학습 집합으로 나머지를 테스트 집합으로 사용한다. S를 번갈아가면서 N번 테스트한다.

  • S의 수가 늘어나면 모델 훈련의 시행 횟수가 증가하게 된다. 이는 훈련이 계산적으로 복잡할 때 문제가 된다.

  • 여러 가지 복잡도 매개변수가 있을 경우 기하급수적인 수의 훈련 실행이 필요할지도 모른다.

  • 이상적인 방식에서는 훈련 집합만을 활용해서 여러 종류의 하이퍼파라미터와 모델의 비교를 한 번의 훈련 과정 동안 시행할 수 있다.

  • 이를 위해 훈련 집합만을 사용하는 성능 척도가 필요하며, 과적합으로 인한 bias로부터 자유로워야 한다.

    

패턴 인식과 머신 러닝(Pattern Recognition and Machine Learning)

 기계 학습의 바이블이라고도 할 수 있는 책이다. 이번에 겨울방학 기간 동안 기계 학습, 딥러닝, 강화 학습에 대해서 공부를 할 예정인데 이 책을 바탕으로 공부를 하며 정리한 내용들을 업로드할 예정이다. 

http://www.kyobobook.co.kr/product/detailViewKor.laf?ejkGb=KOR&mallGb=KOR&barcode=9791188621255&orderClick=LEa&Kc=

문제:

숫자 카드는 정수 하나가 적혀져 있는 카드이다. 상근이는 숫자 카드 N개를 가지고 있다. 정수 M개가 주어졌을 때, 이 수가 적혀있는 숫자 카드를 상근이가 가지고 있는지 아닌지를 구하는 프로그램을 작성하시오.

입력:

첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1<=N<=500,000)이가 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다. 두 숫자 카드에 같은 수가 적혀있는 경우는 없다.

셋째 줄에는 M(1<=M<=500,000)이 주어진다. 넷째 줄에는 상근이가 가지고 있는 숫자 카드인지 아닌지를 구해야 할 M개의 정수가 주어지며, 이 수는 공백으로 구분되어져 있따. 이 수도 -10,000,000보다 크거나 같고, 10,000,000보다 작거나 같다.

출력:

첫째 줄에 입력으로 주어진 M개의 수에 대해서, 각 수가 적힌 숫자 카드를 상근이가 가지고 있으면 1을, 아니면 0을 공백으로 구분해 출력한다.

풀이방법:

 많은 수를 비교해야 하므로 일반 탐색을 사용하면 시간 초과가 발생할 것 같았다. 그래서 로그 단위로 탐색이 가능한 이진탐색을 사용하고자 하였다. 그리고 이진탐색이 가능했던 이유가 같은 수가 적혀있는 경우가 없기도 했다.

 python에 이진탐색을 제공하는 bisect모듈을 사용하였다. bisect.bisect를 사용하면 배열에 값이 있는 위치를 반환하며 이 인덱스는 0부터 시작하는 것이 아닌 1부터 시작한다.(왜 그런진 모르겠다.) 또한 없는 값에 대해서는 그 근처의 값의 인덱스를 반환하기 때문에 bisect로 찾은 값과 내가 찾고자 하는 값이 참일 경우에만 answers의 값을 1로 바꾸도록 하였다.

문제링크:

https://www.acmicpc.net/problem/10815

문제:

정수 N이 주어져 있을 때 이 수가 10보다 크면 일의 자리에서 반올림을 하고, 이 결과가 100보다 크면 다시 10의 자리에서 반올림을 하고, 또 이 수가 1000보다 크면 100의 자리에서 반올림을 하고..(이하 생략) 이러한 연산을 한 결과를 출력하시오.

입력:

첫째 줄에 정수 N이 주어진다. (0<=N<=99,999,999)

출력:

첫째 줄에 위와 같은 연산을 한 결과를 출력하시오.

풀이방법:

뒷자리에서 부터 하나씩 반올림을 하면서 진행하면 된다. 반올림을 하려고 하는 자릿수가 5이면 앞자리에 1을 더해주고, 그렇지 않다면 그 자리를 0으로 바꾼 뒤 그대로 이어붙이면 된다. 그런데 반올림을 하는 자리의 수가 5이상이고 1을 받는 자리가 9이면 문제가 발생한다. 이 경우에는 9가 1을 받아서 10이 되기 때문에 그 앞자리까지에도 영향을 받게 된다. 

이를 int 연산으로 바꾸어서 진행을 했다면 문제가 없겠지만 str의 슬라이싱을 사용해서 문제를 풀고 있기 때문에 이 경우를 따로 예외 케이스로 만들어서 해결해 주도록 한다.

문제링크:

https://www.acmicpc.net/problem/2033

문제:

당신은 FCFS(First-Come, First-Served)의 규칙에 따라 요청된 일을 처리하는 서버를 담당하게 되었다. 매일, 당신은 일을 처리하기 위해 최대 T분 동안 서버에 시간을 할당할 수 있다. 당신은 오늘 주어진 시간동안 몇개의 일이 완료될 수 있는지 알고 싶다.

예시를 들어보겠다. T=180이고, 요청된 일들의 수행시간이 요청된 순으로 45,30,55,20,80,20 분이다. 그러면, 단 4개의 일만이 완료될 수 있다. 처음 4개의 일의 수행시간은 150분으로 주어진 시간 내에 완료될 수 있지만, 처음 5개의 일의 수행시간은 230분으로 주어진 시간 180분보다 크기 때문에 완료될 수 없다. 처음 4개의 일을 수행한 뒤 6번째의 일을 수행해도 T를 초과하지 않지만 5번째 일을 수행할 수 없기 때문에 6번째 일을 수행할 수 없음을 참고해라.

입력:

첫 줄을 두 정수 n과 T이며 (1<=n<=50, 1<=T<=500) n은 일의 개수를 나타낸다. 두 번째 줄은 n개의 100이하의 자연수가 입력되며, 입력된 각 일의 수행 시간을 나타낸다.

출력:

일이 First-come, First-serverd 규칙에 따라 처리될 때, T분 안에 완료될 수 있는 일들의 개수를 출력하라.

풀이방법:

앞에서 부터 더하면서 T를 넘는지 확인하면 된다. T를 넘는다면 break를 걸고 나와서 그 때까지의 값을 출력하면 된다. idx<n이라는 조건이 있는데 이 것은 주어진 일을 모두 T 시간 내에 해결할 수 있을 때 발생하는 에러에 대한 조건이다. while문을 사용했기 때문에 T가 아직 남아 있다면 계속해서 반복하게 될 것이고 런타임에러가 발생한다. 따라서 모든 값을 탐색했다면 종료해야 하기 때문에 이 조건을 넣었다.

문제링크:

https://www.acmicpc.net/problem/10409

문제:

준민이는 탄산 음료를 좋아한다. 탄산 음료를 사느라 돈을 다 써버렸기 때문에, 이제 준민이는 가진 돈이 없어 탄산 음룔를 사먹을 수 없다.

준민이는 항상 법을 지키며 사는 사람이기 때문에, 아무리 탄산 음료가 먹고 싶어도 훔치지 않는다. 따라서, 법적으로 문제가 없는 방법으로 탄산 음료를 구매할 것이다.

마침 빈 병을 특정 개수만큼 가져가면, 새 병으로 바꾸어주는 이벤트가 진행중이다. 준민이는 길에서 빈 병을 열심히 찾은 뒤, 탄산 음료를 먹으려고 한다.

준민이가 현재 가지고 있는 빈 병의 수와 길에서 발견한 빈 병의 수, 새 병으로 바꾸는데 필요한 빈 병의 수가 주어졌을 때, 준민이가 탄산 음료를 몇 개 먹을 수 있는지 구하는 프로그램을 작성하시오.

입력:

첫째 줄에 준민이가 가지고 있는 빈 병의 수 e, 그날 발견한 빈 병의 수 f, 새 병으로 바꾸는데 필요한 빈 병의 개수 c가 주어진다. (e<1000, f<1000,1<c<2000)e,f,c는 모두 음이 아닌 정수이다.

출력:

첫째 줄에 준민이가 탄산 음료를 몇 개나 먹을 수 있는지를 출력한다.

풀이방법:

가지고 있는 빈 병이랑 발견한 빈 병의 수도 중요하지만 이를 통해서 구매한 병의 수도 중요하다. 이 문제의 경우처럼 9개의 빈병으로 3개를 바꿀 수가 있다. 그리고 이 3병을 다 마시면 다시 1병을 바꿀 수 있기 때문에 총 4병이 되는 것이다. 그래서 이와 같은 방법으로 몇번을 더 바꾸어 먹을 수 있는지 모르기 때문에 while을 사용하였다.

병의 수를 c로 나누었을 때 몫을 계속해서 더하며 남은 병과 몫을 다시 더해서 빈 병으로 만든다. 

이 과정을 계속해서 반복하면서 몫이 0이 되는 경우에 빠져 나오도록 하였다.

문제링크:

https://www.acmicpc.net/problem/5032

문제:

서울에서 경산까지 여행을 하면서 모금 활동을 하려 합니다. 여행은 서울에서 출발해 다른 도시를 정해진 순서대로 딱 한 번 방문한 후 경산으로 도착할 예정입니다. 도시를 이동할 때에는 도보 혹은 자전거를 이용합니다. 이때 도보 이동에 걸리는 시간, 도보 이동 시 얻을 모금액, 자전거 이동에 걸리는 시간, 자전거 이동 시 얻을 모금액이 정해져 있습니다. K시간 이내로 여행할 때 모을 수 있는 최대 모금액을 알아보려 합니다

예를 들어 여행 루트가 다음과 같고 K=1,650 일 때,

1, 2번 구간은 도보로, 3번 구간은 자전거로 이동해 모금액을 660으로 하는 것이 가장 좋은 방법입니다. 이때, 1,600시간이 소요됩니다.

solution 함수의 매개변수로 각 도시를 이동할 때 이동 수단별로 걸리는 시간과 모금액을 담은 2차원 배열 travel과 제한시간 K가 주어집니다. 제한시간 안에 서울에서 경산까지 여행을 하며 모을 수 있는 최대 모금액을 return 하도록 solution 함수를 작성하세요.

풀이방법:

동적계획법을 사용해서 풀어야 하는 문제이다. 0번째 인덱스에는 도보로 걸리는 시간, 2번째 인덱스에는 자전거 이동시 걸리는 시간이 담겨 있으며. 1번째, 3번째 인덱스에는 각각 금액이 담겨져 있다. 따라서 0,2번째로 K시간이 넘어가지 않는 선에서 1,3을 더 했을 때 최대가 되는 값을 찾으면 된다.

문제링크:

https://programmers.co.kr/learn/courses/30/lessons/42899

문제:

직사각형 종이를 n번 접으려고 합니다. 이때, 항상 오른쪽 절반을 왼쪽으로 접어 나갑니다. 다음은 n=2인 경우의 예시입니다.

먼저 오른쪽 절반을 왼쪽으로 접습니다.

다시 오른쪽 절반을 왼쪽으로 접습니다.

종이를 모두 접은 후에는 종이를 전부 펼칩니다. 종이를 펼칠 때는 종이를 접은 방법의 역순으로 펼쳐서 처음 놓여있던 때와 같은 상태가 되도록 합니다. 위와 같이 두 번 접은 후 종이를 펼치면 종이에 접은 흔적이 생기게 됩니다.

V 모양이 생긴 부분은 점선(0)으로, ㅅ 모양이 생긴 부분은 실선(1)으로 표시했습니다.

종이를 접은 횟수 n이 매개변수로 주어질 때, 종이를 절반씩 n번 접은 후 모두 펼쳤을 때 생기는 접한 부분의 모양을 배열에 담아 return 하도록 solution 함수를 완성해주세요.

풀이방법:

이 문제는 종이접기 수열을 사용하는 문제이다. 종이접기 수열이란 이 문제처럼 종이를 일정한 방향으로 접었을 때 생기는 굴곡에 대한 수열이다. 

이 문제처럼 오른쪽에서 왼쪽으로 접는 경우에는 가운데가 0으로 고정되어서 수열이 생성된다.

1 ->  0

2 ->  0 + 0 + 1

3 ->  0 + 0 +1 + 0 +0 + 1+ 1

4 -> 001+0+011 + 0 + 001+1+011

5 -> 0010011+ 0 + 0011011 + 0 +0010011 + 1 + 0011011

....

1, 2, 3에서는 규칙을 찾기 어렵지만 4부터는 규칙을 찾을 수 있다.

가운데 0을 기준으로 이전 단계의 모양이 반복되는 것을 알 수 있다. 가운데 0을 기준으로 했을 때 왼쪽은 이전단계의 중간이 0인 경우 오른쪽은 이전단계의 중간이 1인 경우이다. 따라서 1, 2의 경우에는 예외처리로 두어서 답을 반환하도록 하고, 3부터는 반복문을 통해서 규칙을 생성하도록 하였다.

문제링크:

https://programmers.co.kr/learn/courses/30/lessons/62049