CodeDrive

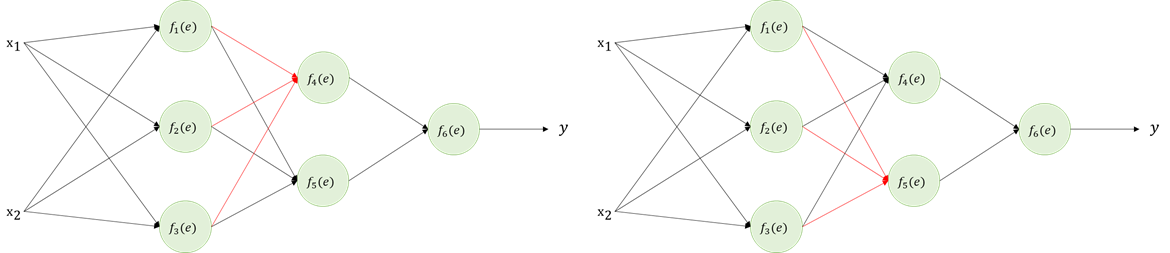
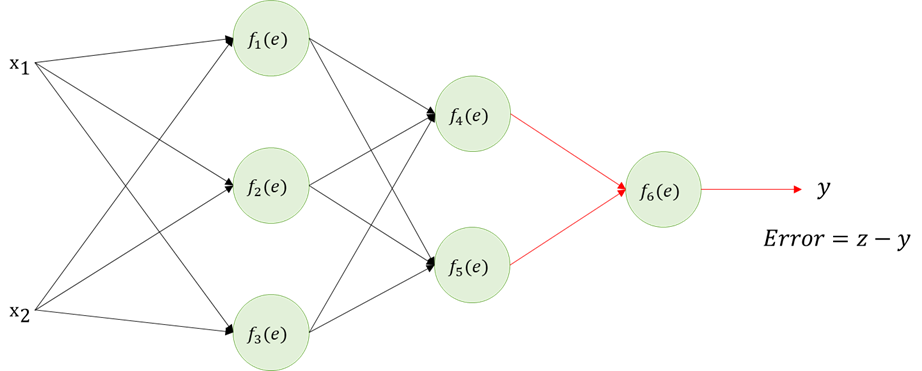
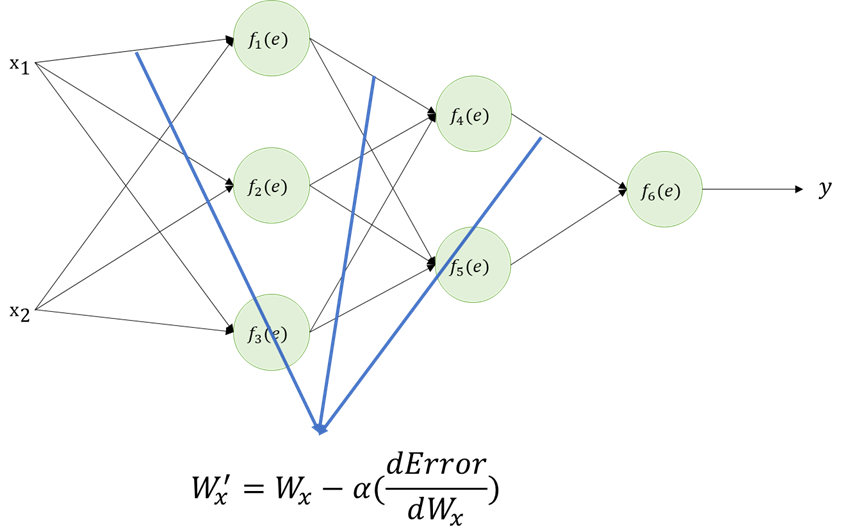
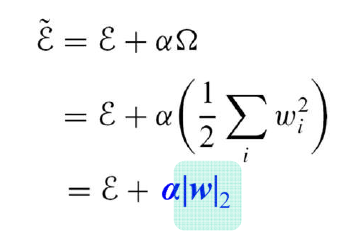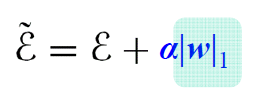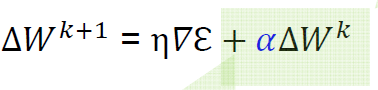Lecture 3

Basic

• Overview of CNNs
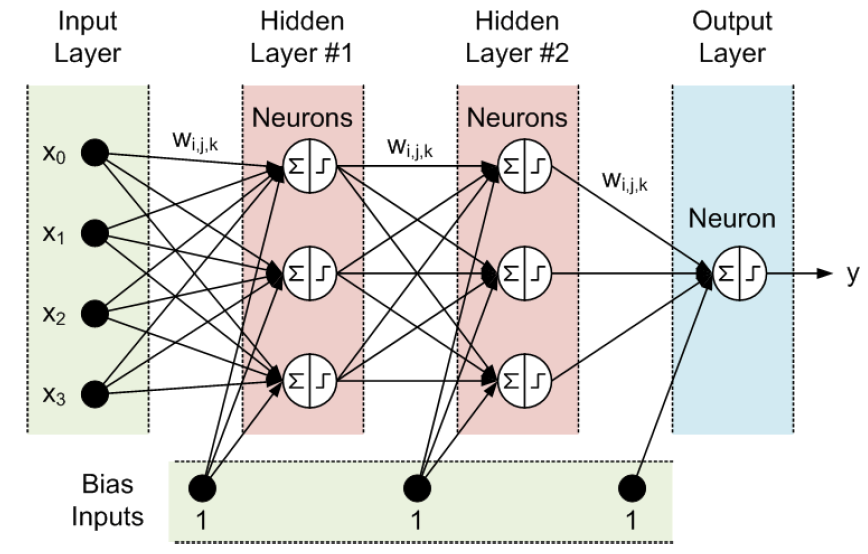
  • A special case of MLP
  • Commonly apply to visual object or 2D array input
  • Unified feature extractor and classifier in one network
  • Filter kernel = weights in between layers
  • Feature map = filtered outputs

• How can compute Feature Map Size?

  

  • i = input size, k = filter size(kernel), s = stride, o = output feature map size

  • if o<i, can occur some problem

    • then, we can use Zero Padding

      

• At same points, we can apply multiple filters. We call it "channel"

Two Characteristics of CNNs

1. Local Connectivity - image is locally correlated
2. Weight Sharing- overcome enormous weights problem

Local Connectivity

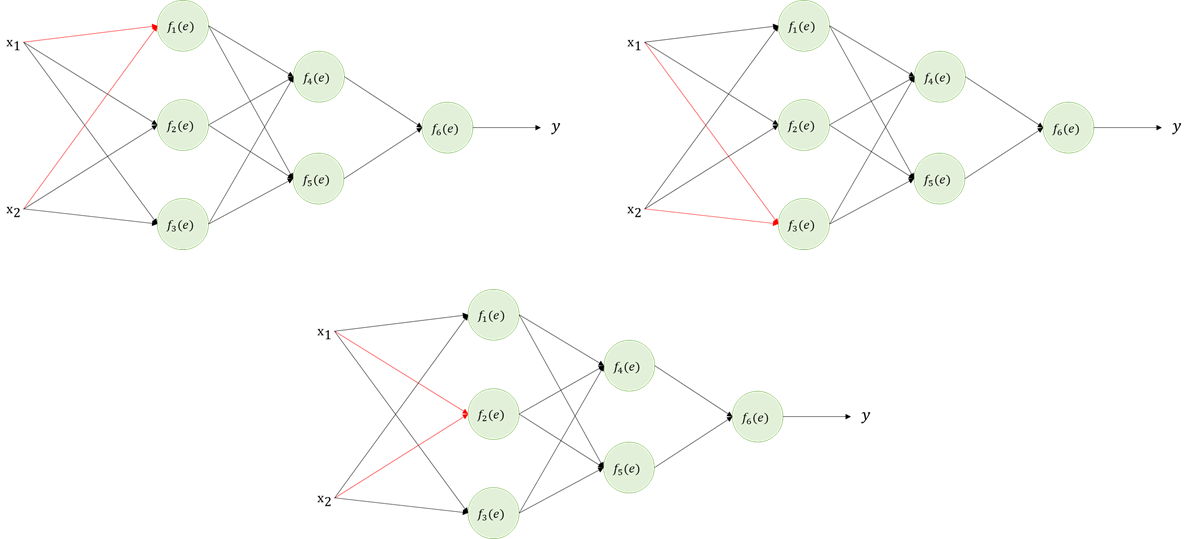
• MLP : Weights are fully connected, ie. MLP use all weights
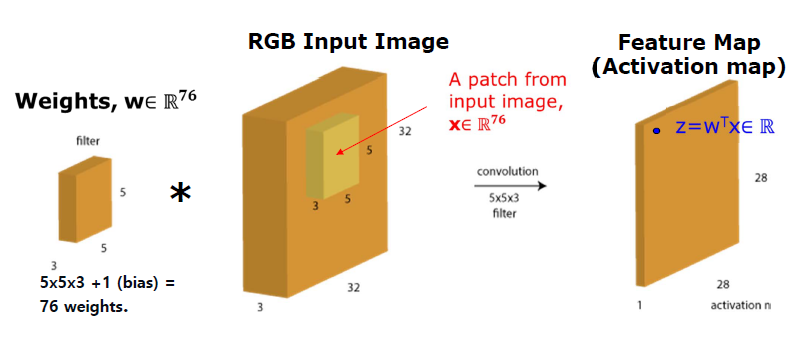
• CNNs : One neuron will connect to filter size chunk , thus only have 5x5x3 weights

Receptive Field(RF)

How much a convolution window "see" on it's input image or part of the image that is visible to one filter at a time

In upper figure, dark pink square in left light pink square(32x32x3) is Receptive Filed.

It means "Receptive Filed size == filter size"

• How the later feature map "see" the image?

Weight Sharing

• MLP has different weights for every single neuron.
  • Total # of weights = (filter size) x (Input_w x Input_h x # of feature maps) = too many!
• CNN has same weight for every single feature map
  • Total # of weights = (filter size) x # of feature maps = small than MLP

Max Pooling

Pooling does resize the activation map from convolution to get new layer.

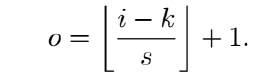
• Output size (o)
• Input size (i)
• Pooling window size (k)
• Stride (s)

Fully Connected (FC) layer

• FC layer started right after the last convolution or pooling layer
• Flatten pooling layer = input layer of MLP
• Last FC layer = output layer of ConvNet. It uses several tasks like classification.

Summary

Typical ConvNet process : [CONV layer - ReLU-Pooling] x N - [FC-ReLU] x M - FC - (softmax or sigmoid)

• Parameter in CNN

  • Conv layer
    • Filter window size (Odd number)
    • Number of Filters (Power of 2)
    • Stride
    • # of Conv layers
  • Pooling layer
    • Pooling window size
    • stride
    • # of pooling layer
  • Fc layer
    • # of hidden nodes
    • # of FC layer
  • BP algorithm
    • Learning rate, batch number, momentum coefficient, L2 coefficient

  Feature Normalization in CNN

  Batch Normalization(BN)

  • Using mean and variance of each feature, Normalize each feature in batch
  • normalize feature map of each channel over a batch sample

  Layer Normalization(LN)

  • Using mean and variance of each feature in input, normalize each input in batch
  • applicable to dynamic network and recurrent network(good)
  • normalize entire feature map

  

  Instance Normalization

  • It is similar with LN but not applicable to MLP and RNN. It is best for CNNs.
  • Effective for style transfer and image generation tasks using GAN
  • Compute mean and variance each sample in each channel

  Group Normalization

  • It is similar with Instance Normalization but not applicable to MLP and RNN. It is best for CNNs.
  • Effective for object detection, video classification (It is effective in memory problem)
  • Compute mean and variance each sample in each group that channels are grouped by group size g.
  • In image, The center of image and edge of image do not have equal meaning.
    • Thus, We can get flexibility if we compute differently each channels.
    • Also, Image's channel is not independent. If we use some channels nearby pivot channel, we can apply normalization at large region.

Storage and Computational Complexity

• c_i-1 = previous layer channel number
• c_i = previous layer channel number
• m_i-1 = previous feature map size
• m_i = previous feature map size
• k = filter size

# weights for layer i = (k x k x c_i-1) xc_i

# memory of layer i = m_i x m_i x c_i

# FLOPs = (kxk) x(m_i x m_i) x (c_i-1 x c_i)

CNNs Variants

Legends

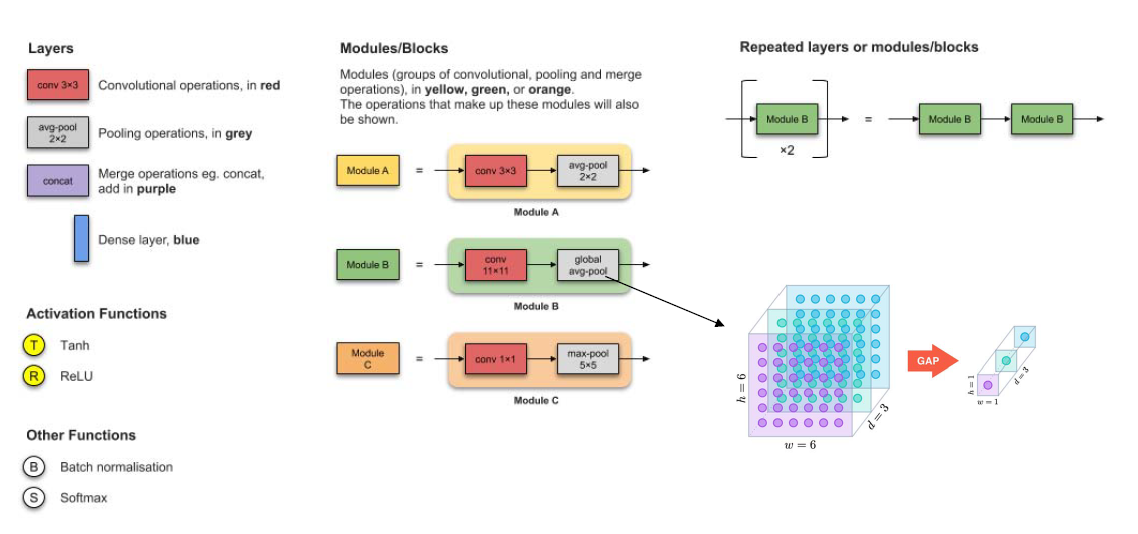
LeNet 5 (1998)

• This architecture has become the standard
  • Stacking ConvNet and pooling
  • ending network with one or more fc.

AlexNet(2012)

• Apply RelU, pooling, data augmentation, dropout, Xavier initialization

VGGNet - 16 (2014)

• use only 3x3 sized filter.
• Before VGGNet, they use large filter. But 3x3 sized filter can result same output if use mulitple filter compared with large sized filter.

Effects of 3x3 sized filter

1. Decrease number of weights
   • If we have an input which has size [50x50x3] and 5x5 sized filter, # of weight is 5x5x3 = 75
   • If 3x3 sized filter, # of weight is (3x3x3)+(3x3x1) = 27 + 9 = 36
     • 2 consecutive 3x3 filters are same as 5x5 filter
2. Increase non-linearity
   • Each convolution has ReLU. 3x3 sized filter model has more non-linear function like ReLU than large sized filter model.

GoogleNet Inception-V1 (2014)

• 22 layers and 5 Million weights in total

• GoogleNet contains Inception Module that has parallel towers of convolutions with different filters, followed by concatenation, which captures different features at 1x1, 3x3 and 5x5.

  • In Inception Module, use 1x1 filter before 5x5 filter or 3x3 filter because if we don't use 1x1 sized filter, will get too many weights!

• We call 1x1 filter "bottleneck structure".

  • 1x1 convolutions are used for dimensionality reduction to remove computational bottlenecks
  • 1x1 convolutions add nonlinearity within a convolution

• Auxiliary classifier

  • Deeper network layers, higher likelihood of vanishing gradient.
  • Encourage discrimination in the lower stages
  • It only uses in training time.

ResNet-50 (2015)

• Skip connections/identity mapping can make deep network
• use batch normalization
• Remove FC layer and replace with GAP(Global Average Pooling)

Motivation

• When networks go deeper, a degradation problem has been exposed.
  • 56-layer's result is worse than 20-layer
  • But deep layer model has good results in many times.
    • So, need some techniques to make deep-layer model

Why ResNet works?

• use identity mappings to approximate "shallow network"

  

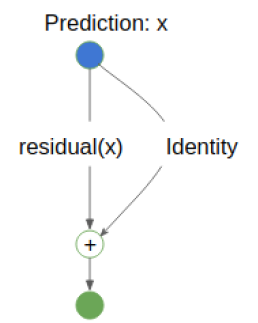
• Advantages of Skip Connection

  • Reduce optimization difficulty of deeper networks
  • Alleviate gradient vanishing problem
  • Reuse lower level feature

Xception (2016)

• An adaptation from Inception where the Inception modules have been replaced with depthwise separable convolution(DS-convolution layers)
  • Xception has same number of parameters as Inception

Inception - ResNet-V2 (2016)

• Converting Inception modules to Residual Inception blocks

ResNext-50 (2017)

• Adding of parallel towers/branches/paths within each module.

DenseNet (2017)

• Dense blocks where each layer is connected to every other layer in feedforward fashion
  • Alleviates vanishing gradient

Squeeze and Extraction - SENet (2017)

• Squeeze and Extraction can do feature recalibration to feature maps from origin networks.
• It is not a complete network, but a wrapper. Thus, we can use it with ResNet, ResNext, Inception etc.
• Improve channel interdependencies at almost no computational cost.

Squeeze

• Get a global understanding of each channel by squeezing the feature maps to a single numeric value.
  • use GAP(Global Average Pooling)

Extraction

• Feature Recalibration to computer channel-wise dependencies.
  • using Fully connected layer and non-linear function.

Lecture 2

• Generalization
• Speed of Convergence for Training and Learning quality

Performance Generalization

Neural network는 두 가지 중요한 점을 충족시켜야 한다.

1. training data를 통해서 학습하기 때문에, training data에 대해서는 정확하게 분류해야 한다.
2. learning process에 대해서 generalize하기 위해서 이전에 보지 못한 데이터(test data)에 대해서도 잘 분류해야 한다.

복잡한 결정 경계선(면)을 가지고 있다고 해서 이 것이 좋은 generalization performance를 가지고 있다고 하지 않는다.

실험 과정에서는 다음과 같이 진행된다.

1. data set을 Learning set(85%)과 test set(15%)으로 구분한다.
2. Learning set을 training set(70%)와 validation set(15%)로 구분을 한다.
3. training set으로 network을 훈련을 하고, training set과 validation set으로 성능을 평가한다.

만약 training error가 높다면 underfitting이 발생한 것이고, training error가 낮지만 validation error가 높으면 overfitting, 둘 다 낮은 수치가 나온다면 generalization이 잘 일어난 것을 의미한다.

위에서 했던 것에서 더 발전시켜서 3번을 서로 다른 구조로 진행한다.

4. 3번의 여러 구조에서 over and underfit이 아닌 best network을 고른다.
   • 다른 model인 것이 아니라 parameter tuning을 하는 것
5. 이를 learning set으로 다시 훈련을 한다.
6. test set으로 generalization을 테스트 한다.

• three subset을 바꿔가면서 N번 반복하는 것을 N-fold cross validation protocol이라고 한다.
• 하지만 각 parameter별로 best value가 다르다면...?

Parameter search

1. training set으로 다른 parameter들을 train하고, validation으로 평가한다.
2. 각 parameter에 대해서 error_val을 기록한다.
3. training set과 validation set을 reshuffle을 해서 1과 2를 반복한다.
4. 3번을 n times 반복한다.(n-fold CV)
5. n-fold로 부터 얻은 error_val 평균내고, 작은 평균 error_val을 가진 것들을 모아서 best parameter set을 만든다.

• Parameter searching 전략에는 다음 두 가지가 있다.
  • Grid Search
    • q개의 파라미터가 있고, 각 파라미터당 p개의 value가 생긴다면 이 경우에 대해서 모두 탐색하는 것을 의미한다.
    • mp^q개다.
  • Random Search
    • parameter value들을 random combination으로 진행한다.
    • grid search보다 좋은 점은 each parameter마다 unique한 value를 얻을 수 있기 때문에 좋다??

Generalization

generalization을 위해서 적절한 모델을 고르는 것도 중요하지만 다른 방법들에는 어떠한 것이 있을 까?

1. Enrich Training data

적은 데이터를 가지고 있으면, 모델은 쉽게 수렴할 수 있다.(small training error) 적은 데이터를 모델이 전부 외어버린다고 생각하면 된다. 하지만 절대적인 정보의 양이 부족하기 때문에 나쁜 generalization을 가진다.(large training error)

거대한 데이터라면 모델이 이를 학습하기 위해서 더 많은 노력을 해야 한다. (higher training error) 대신 정보의 양이 충분해졌기 때문에 더 좋은 generalization 성능을 가질 것이다.(lower test error)

즉, 질이 좋고 많은 양의 데이터를 사용해야 overfitting을 방지할 수 있다. 하지만, 이러한 데이터를 구하는 것은 많은 비용이 들고, 힘들다.

그래서 인공적으로 training data를 늘리는 방법을 사용하는데, 이를 Data augmentation이라고 부른다. (translation, rotation, stretching, shearing, lens distortions...)

2. Early stopping

훈련을 진행할 때, 언제 멈추는 것이 좋을까? 훈련을 계속해서 진행을 한다면 zero training error를 달성할 수 있을 것이다. 하지만 이는 train data에 overfitting 된 상태이기 때문에 test error는 매우 높을 것이다. 따라서 validation error를 기준으로 early stopping 할 포인트를 구한다.

3. Ensemble

여러 Network를 동시에 훈련을 시키고, 이들의 average를 사용하는 방법이다.

4. Regularization

network의 complexity를 줄이는 방법이다.

• L2(weight decay)

  

  • 각각의 벡터에 대해 항상 unique한 값을 반환

• L1

  

  • 특정 feature가 없어도 같은 값을 반환
  • feature selection이 가능하다.
  • Sparse model이 적합하다.
  • 미분 불가능한 점이 있기 때문에 gradient에 주의해야 한다.

• Max norm constraints

  • weight vector에 upper bound를 설정하는 것이다. (미분값도 제한된다.)
  • learning_rate를 크게 잡더라도 explode 하지 않는다.

• Dropout

  • 위에서 소개한 정규화 방법들과 같이 사용할 수 있다. random 하게 hidden node와 input node를 제거하고(off하고) 이들은 weight를 업데이트 하지 않는다.
  • 이는 training 과정에서만 적용되고, prediction에서는 dropout을 사용하지 않는다.

Speed of Convergence

• batch training
• Momentum term
• weight initialization
• learning rate
• activation functions
• feature normalization and scaling
• batch normalization(BN)

일반적인 BP(backpropagation)은 saddle point나 local minimum에 약하다는 단점이 있다.

• momentum term
  • gradient update에 관성을 부여한다는 아이디어다.
  • 기존 BP는 다음 식에 따라서 업데이트 된다.

    • 

  • momemtum term은 이전 weight update 한 값을 일부 제해서 더해준다.

    • 

    • a가 0이라면 일반적인 backpropagation과 동일하다.
    • a가 1이라면 gradient descent는 완전히 무시되고, mometum에 의해서만 업데이트 된다.
    • 보통 0.9나 0.95를 많이 사용한다.
• weight Initialization
  • 초기에 weight를 어떻게 init하는지에 따라서 성능이 바뀐다. 적절한 값을 사용해야 한다.
  • Xavier Initialization을 사용한다.
• Learning rate
  • 적절한 learning rate를 골라야 한다.
    • 너무 작게 고르면 늦게 수렴할 수 있다.
    • 너무 크게 고르면 발산 할 수 있다.
  • Adagrad, RMSprop, ADAM, ...
• Activation function
  • simoid나 tanh같은 경우에는 미분값을 자주 곱할수록 작아지기 때문에 gradient vanishing 문제가 발생한다.
  • 따라서 ReLU를 사용한다.
    • 장점
      • simple하고, positive region에서는 stable하다.
      • 수렴속도도 따르다.
      • sparsifcaiton을 허용한다.
    • 단점
      • gradient가 0보다 작은 값이 많다면 Dying 할수도 있다.
        • Leaky ReLU, Parametric ReLU와 같은 걸로 해결 가능
• Feature Normalization
  • 각 feature들의 range가 다르기 때문에 normalization을 수행한다.
  • Max-min normalization
  • Z score normalization
  • PCA - large dataset에는 부적합
• Batch Normalization (BN)
  • 각 layer마다 input의 distribution이 달라지는 것을 막기 위함이다.
  • pre-activation, post-activation에 각각 normalizing을 수행한다.
  • 이는 mini-batch 단위로 수행히 가능하고, 각각 독립적으로 수행할 수 있다.
  • prediction을 위해서는 re-adjust해야 하고, r과 b도 알아야 한다.
  • 장점
    • high learning rate가 가능하다.
    • deep network에 사용 가능하다.
    • weight init에 민감하지 않다.
  • 단점
    • Batch number가 커야 한다.
    • dynamic network 구조나 recurrent network에 적합하지 않다.

Summary

• good convergence를 가장 우선적으로 생각해야 하지만 good generalization을 보장하진 않는다.
• convergence의 속도를 향상시키기 위해서 여러 방법들을 사용할 수 있다.

Lecture1

• Multiple Layer Perceptron(MLP)
• Loss Function
  • Mean Square Error
• Backpropagation Algorithms
  • Stochastic Gradient Descent(SGD)
  • Batch Gradient Descent(BGD)
  • Mini-batch GD

Multiple Layer Perceptron

하나의 Neuron은 이전 Neuron들의 값과 weight 간의 곱의 합들을 구한 뒤 activation function인 f를 통과해서 y를 만들어 낸다.

layer들은 이러한 Neuron들을 여러 개 가지고 있는 것을 의미하고, 이러한 layer가 여러 개 존재한다면 이를 Multiple Layer Perceptron(MLP)라고 부른다.

Input layer는 x_i 만큼의 입력값이 존재하고, Hidden Layer가 앞서 말한 연산을 수행한다. Output Layer는 하나의 값을 계산하기 때문에 하나의 Neuron이 존재한다.

Activation function

각 hidden node에 적용되는 activation function은 다음과 같은 것들이 있고, 이들의 대한 설명은 다음에 기회가 있으면 하도록 한다.

• Sigmoid Function
• 
• Hyperbolic Tangent
• 
• Rectifier Linear(ReLU)
• 

Usage

MLP는 Classification, Regression 등에서 사용될 수 있다.

Loss Function For MLPs

Loss Function은 참값과 예측값과의 차이를 의미하기 때문에 MLP에서 Supervised Learning 학습 방법에서 나타난다.

그림으로 프로세스를 보면 다음과 같이 설명할 수 있다.

In Regression

MLP의 output layer에서 Linear function을 사용한다. loss function은 각 output error의 square들의 합으로 구성된다. 이를 Mean Square Error(MSE)라고 부르고, 식으로 표현하면 다음과 같다.

In Classification

MLP의 output layer에서 Softmax function을 사용한다. softmax는 Hard max function과는 다르게 exp()함수를 사용하는데, 그 이유는 더 큰 logit을 가지고 있는 값에 더 큰 값을 부여하기 위함이다. Loss function은 Average Cross-Entropy (ACE) loss를 사용한다.

t_i는 true label, f(s)_i는 softmax output을 의미한다.

Backpropagation

Gradient Descent는 weight를 기울기 반대 방향으로 업데이트 하면서 Optimal weight를 찾아가는 과정이다. 이 때 기울기 반대 방향으로 업데이트 할 때, learning rate를 적절한 값으로 설정해야 한다. 만약 너무 learning rate가 작다면 local minimum에 빠질 수 있고, 훈련속도가 너무 느릴 수 있다. 하지만 크다면 shooting이 발생할 수 있어 발산할 수도 있다.

역전파 하는 과정을 그림과 함께 보면 다음과 같이 표현할 수 있다.

위 그림과 같은 간단한 Two-Hidden layers MLP가 존재한다고 하자. 이 때, x는 input, y는 output을 의미하며 f 함수는 sigmoid라고 가정하자.

Forward

우선 x로부터 y를 얻기 위해 forwarding 과정을 거친다. x는 빨간 선을 따라서 y를 얻을 수 있다.

예측값 y를 얻으면 실제값 z와 비교해서 Error를 얻을 수 있다.

Backpropagation

이제 Error 오차를 얻었으니 각 노드에서 온 값들이 얼마나 영향을 주었는지 거꾸로 탐색하며 Error의 정도를 측정한다.

Forward되는 과정에서 w를 통하여 y로 도달했기 때문에 Error 또한 weight만큼의 영향을 주었다고 생각할 수 있다. 이 때, w_i,j는 i에서 j로 향하는 weight를 의미한다. 위 그림과 같은 과정을 input x 까지 계속해서 반복한다.

Weights Updating

Backpropagation 과정을 거쳤으면 각 weight별로 얼만큼의 에러를 발생했는지 확인했기 때문에 다음 예측을 정확히 하기 위해서 weight를 변경해야 한다. 이전 단계에서 구했던 Error를 편미분 하여서 weight를 update하도록 한다.

BP Training

1. Stochastic GD (SGD)
   • 각 single instance에 대해서 local error를 계산하고(like SE or CE) gradient를 계산한다.
   • solution에 도달하기까지 많은 시간이 걸린다.
   • 하지만 빠르다
2. Batch GD (BGD)
   • 전체 데이터를 가지고 global error를 계산한다.(like MSE or ACE) global error gradient를 계산해서 한번에 업데이트 한다.
   • 많은 계산량을 요구한다.(그래서 느리다.)
   • 소규모 훈련 데이터에 사용가능하다.
3. Mini-batch GD
   • 1번과 2번의 장점을 합친 것이다.
   • B=1이면 SGD가 되고, B=Q가 되면 BGD가 된다.