Lecture1
- Multiple Layer Perceptron(MLP)
- Loss Function
- Mean Square Error
- Backpropagation Algorithms
- Stochastic Gradient Descent(SGD)
- Batch Gradient Descent(BGD)
- Mini-batch GD
Multiple Layer Perceptron
하나의 Neuron은 이전 Neuron들의 값과 weight 간의 곱의 합들을 구한 뒤 activation function인 f를 통과해서 y를 만들어 낸다.

layer들은 이러한 Neuron들을 여러 개 가지고 있는 것을 의미하고, 이러한 layer가 여러 개 존재한다면 이를 Multiple Layer Perceptron(MLP)라고 부른다.
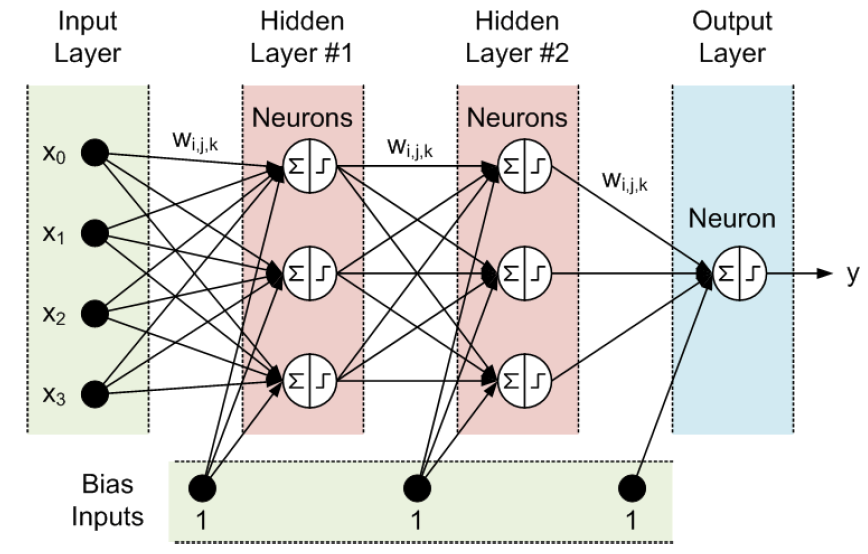
Input layer는 xi 만큼의 입력값이 존재하고, Hidden Layer가 앞서 말한 연산을 수행한다. Output Layer는 하나의 값을 계산하기 때문에 하나의 Neuron이 존재한다.
Activation function
각 hidden node에 적용되는 activation function은 다음과 같은 것들이 있고, 이들의 대한 설명은 다음에 기회가 있으면 하도록 한다.
- Sigmoid Function

- Hyperbolic Tangent

- Rectifier Linear(ReLU)

Usage
MLP는 Classification, Regression 등에서 사용될 수 있다.
Loss Function For MLPs
Loss Function은 참값과 예측값과의 차이를 의미하기 때문에 MLP에서 Supervised Learning 학습 방법에서 나타난다.
그림으로 프로세스를 보면 다음과 같이 설명할 수 있다.
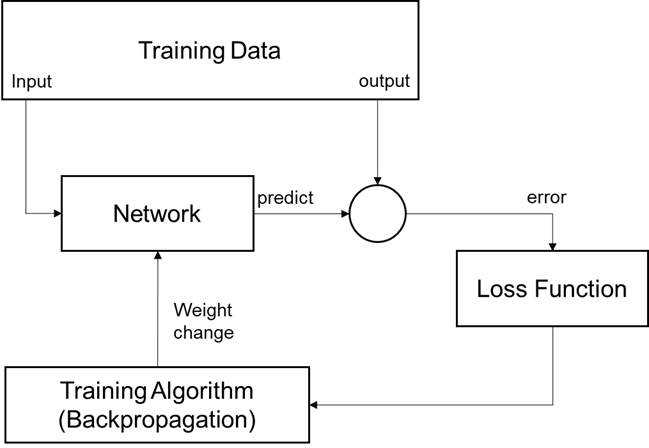
In Regression
MLP의 output layer에서 Linear function을 사용한다. loss function은 각 output error의 square들의 합으로 구성된다. 이를 Mean Square Error(MSE)라고 부르고, 식으로 표현하면 다음과 같다.
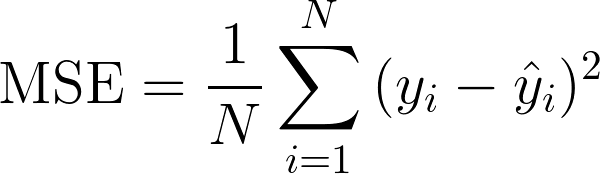
In Classification
MLP의 output layer에서 Softmax function을 사용한다. softmax는 Hard max function과는 다르게 exp()함수를 사용하는데, 그 이유는 더 큰 logit을 가지고 있는 값에 더 큰 값을 부여하기 위함이다. Loss function은 Average Cross-Entropy (ACE) loss를 사용한다.
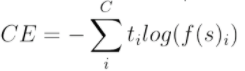
ti는 true label, f(s)i는 softmax output을 의미한다.
Backpropagation
Gradient Descent는 weight를 기울기 반대 방향으로 업데이트 하면서 Optimal weight를 찾아가는 과정이다. 이 때 기울기 반대 방향으로 업데이트 할 때, learning rate를 적절한 값으로 설정해야 한다. 만약 너무 learning rate가 작다면 local minimum에 빠질 수 있고, 훈련속도가 너무 느릴 수 있다. 하지만 크다면 shooting이 발생할 수 있어 발산할 수도 있다.
역전파 하는 과정을 그림과 함께 보면 다음과 같이 표현할 수 있다.

위 그림과 같은 간단한 Two-Hidden layers MLP가 존재한다고 하자. 이 때, x는 input, y는 output을 의미하며 f 함수는 sigmoid라고 가정하자.
Forward
우선 x로부터 y를 얻기 위해 forwarding 과정을 거친다. x는 빨간 선을 따라서 y를 얻을 수 있다.
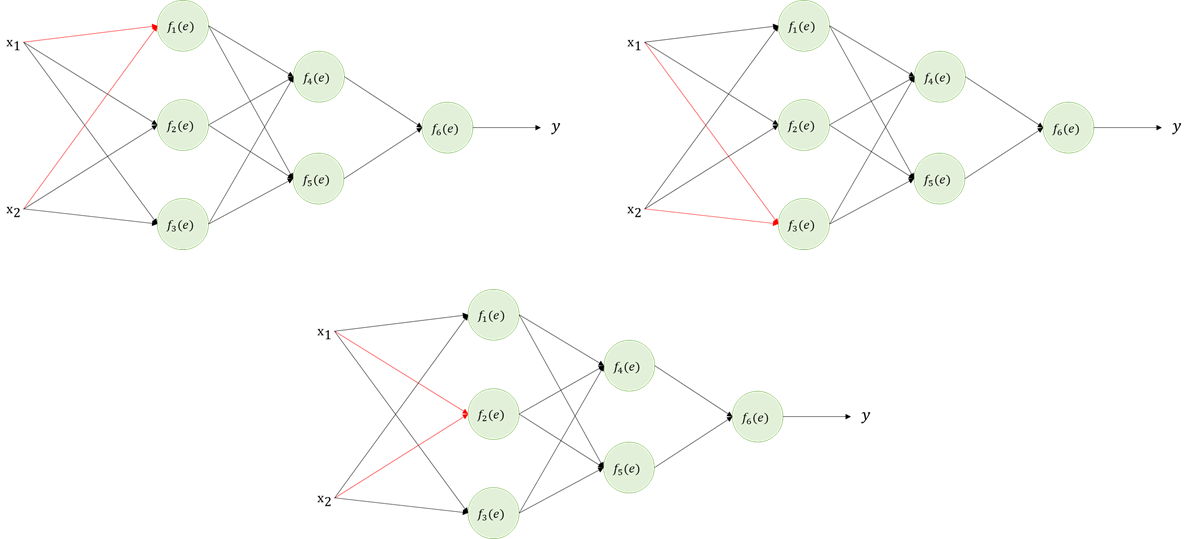
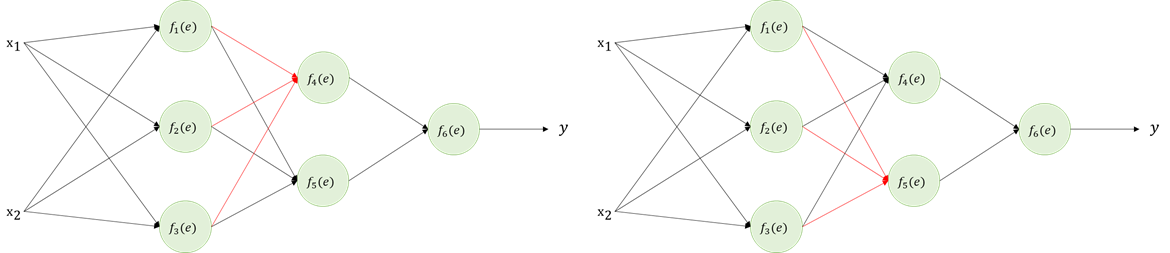
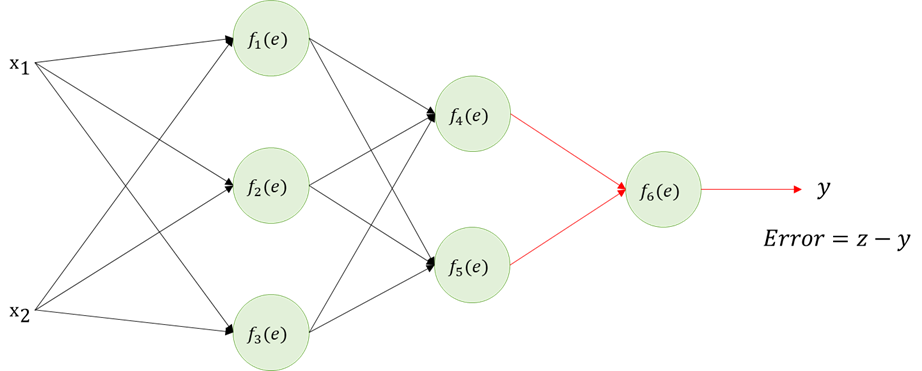
예측값 y를 얻으면 실제값 z와 비교해서 Error를 얻을 수 있다.
Backpropagation
이제 Error 오차를 얻었으니 각 노드에서 온 값들이 얼마나 영향을 주었는지 거꾸로 탐색하며 Error의 정도를 측정한다.

Forward되는 과정에서 w를 통하여 y로 도달했기 때문에 Error 또한 weight만큼의 영향을 주었다고 생각할 수 있다. 이 때, wi,j는 i에서 j로 향하는 weight를 의미한다. 위 그림과 같은 과정을 input x 까지 계속해서 반복한다.
Weights Updating
Backpropagation 과정을 거쳤으면 각 weight별로 얼만큼의 에러를 발생했는지 확인했기 때문에 다음 예측을 정확히 하기 위해서 weight를 변경해야 한다. 이전 단계에서 구했던 Error를 편미분 하여서 weight를 update하도록 한다.
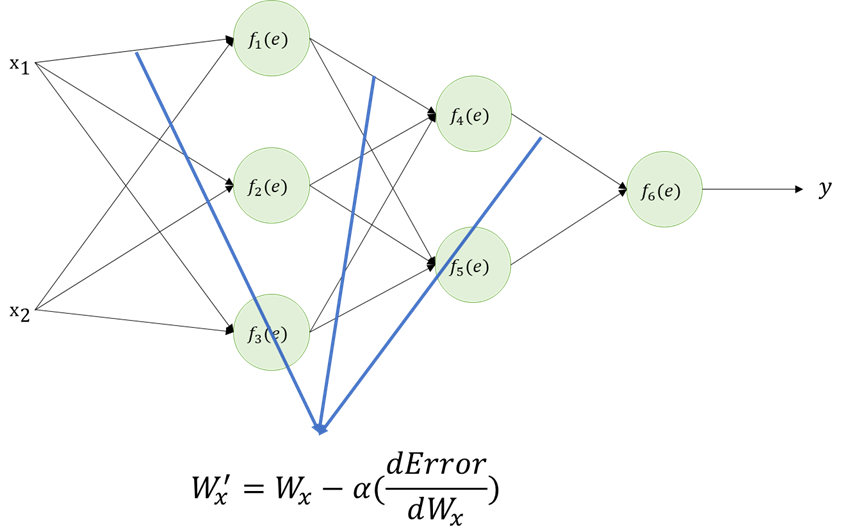
BP Training
- Stochastic GD (SGD)
- 각 single instance에 대해서 local error를 계산하고(like SE or CE) gradient를 계산한다.
- solution에 도달하기까지 많은 시간이 걸린다.
- 하지만 빠르다
- Batch GD (BGD)
- 전체 데이터를 가지고 global error를 계산한다.(like MSE or ACE) global error gradient를 계산해서 한번에 업데이트 한다.
- 많은 계산량을 요구한다.(그래서 느리다.)
- 소규모 훈련 데이터에 사용가능하다.
- Mini-batch GD
- 1번과 2번의 장점을 합친 것이다.
- B=1이면 SGD가 되고, B=Q가 되면 BGD가 된다.
'Lecture Note > DeepLearning' 카테고리의 다른 글
| Lecture 3. Convolution Neural Network and its Variants (0) | 2021.06.30 |
|---|---|
| Lecture 2. Network Implementation (0) | 2021.06.16 |