문제:
아래의 그림과 같이 높은 빌딩 사이를 따라 좁은 길이 나있다. 두 개의 사다리가 있는데 길이가 x인 사다리는 오른쪽 빌딩의 아래를 받침대로 하여 왼쪽 빌딩에 기대져 있고 길이가 y인 사다리는 왼쪽 빌딩의 아래를 받침대로 하여 오른쪽 빌딩에 기대져 있다. 그리고 두 사다리는 땅에서부터 정확하게 c인 지점에서 서로 교차한다. 그렇다면 두 빌딩은 얼마나 떨어져 있는 걸까?

입력:
첫째 줄에 차례대로 x,y,c에 해당하는 양의 실수 세 개가 입력된다. 수는 소수점 여섯째 자리까지 주어질 수 있다.
출력:
두 빌딩사이에 너비가 되는 수치를 출력한다. 절대/상대 오차는 10^-3까지 허용한다.
풀이방법:
이분 탐색을 기반으로 하지만 수학적인 내용이 더 많이 들어가는 문제인 것 같다. 문제의 기본 틀은 두 빌딩 사이의 거리를 d라고 했을 때, 이를 이분 탐색으로 값을 바꾸어 간다. 임의의 d에 따라서 사다리가 교차하는 높이 h가 달라질 것이다. 따라서 이분탐색을 통해서 그 중 c와 같아지는 d를 찾도록 한다.
임의의 d에 따라서 h를 구하는 방법은 수학의 닮음을 사용하도록 해야 한다. 사다리가 교차하는 높이를 h라 하고 선을 다음과 같이 그리면 닮음 꼴인 직각 삼각형을 얻을 수 있다.
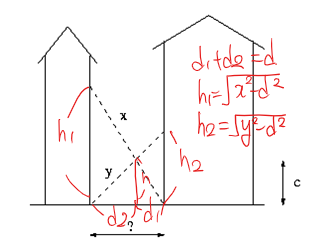
h라는 직선이 생김에 따라 d도 d1과 d2로 나뉘게 될 것이고, h1과 h2도 다음과 같이 정의를 할 수 있을 것이다.
그러면 빗변이 x인 삼각형과 y인 삼각형에 각각 다음과 같은 닮음비를 얻을 수 있다.
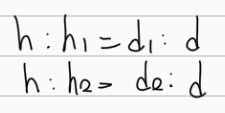
우리가 최종적으로 원하는 변수는 h이기 때문에 h=( ~ ) 와 같은 형태로 변형시켜야 할 것이다. 그러기 위해서는 d1+d2 = d임을 알고 있기 때문에 이를 활용해서 변수를 줄이도록 하자.
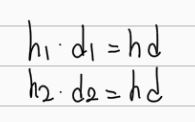

그러기 위해서는 일단 닮음비를 정리해서 d1과 d2에 관한 식으로 만들었다. 그리고 난 뒤에 위 두 식을 더한다면 d1과 d2를 d로 바꿀 수 있게 될 것이다.

이제 양변을 각각 d로 나눌 수 있을 것이다. d는 두 빌딩 사이의 거리이므로 0을 초과한 거리일 것이다. 따라서 양변을 나누는 것에 문제가 없다.

그러면 위 그림의 제일 위의 식과 같이 얻을 수 있을 것이고 좌변을 h에 대해서 묶을 수 있게 될 것이다. 좌변을 h로 묶고 난 뒤에 남은 것들을 우변으로 넘겨준다면 이를 h에 대한 식으로 만들 수 있을 것 이다. 따라서 위 그림의 두번째와 세번째 식은 그 과정을 담고 있다.
h1과 h2는 x, y, d로 이루어진 변수이기 때문에 정확한 값을 계산할 수 있다. (d는 이분 탐색으로 정해진 값이다.) 따라서 h의 값을 구할 수 있을 것이고 이를 c와 비교하면서 c에 근접하게 d를 이분탐색으로 찾을 수 있을 것이다.
그렇게 찾은 mid값을 소숫점 셋째 자리까지 반올림해서 출력하도록 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
import math
x,y,c=map(float,input().split())
left,right=0,min(x,y)
while(abs(right-left)>1e-6):
mid=(left+right)/2.0
d=mid
h1=math.sqrt(x*x-d*d)
h2=math.sqrt(y*y-d*d)
h=(h1*h2)/(h1+h2)
if h > c:
left=mid
else:
right=mid
print("%.3f"%round(mid,3))
|
cs |
문제링크:
https://www.acmicpc.net/problem/2022
'Algorithm > Python' 카테고리의 다른 글
| [BOJ]14889. 스타트와 링크 (0) | 2019.09.23 |
|---|---|
| [BOJ]1697. 숨바꼭질 (0) | 2019.09.22 |
| [BOJ]1561. 놀이공원 (0) | 2019.09.20 |
| [BOJ]1080. 행렬 (0) | 2019.09.19 |
| [BOJ]10610. 30 (0) | 2019.09.18 |