문제:
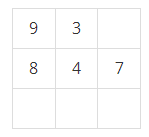
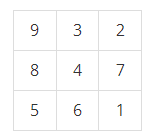
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절히 뽑으면, 그 뽑힌 정수들이 이루는 집합과, 뽑힌 정수들의 바로 밑의 둘째 줄에 들어있는 정수들이 이루는 집합이 일치한다. 이러한 조건을 만족시키도록 정수들을 뽑되, 최대로 많이 뽑는 방법을 찾는 프로그램을 작성하시오. 예를 들어, N=7인 경우 아래와 같이 표가 주어졌다고 하자.

이 경우에는 첫째 줄에서 1, 3, 5를 뽑는 것이 답이다. 첫째 줄의 1, 3, 5밑에는 각각 3, 1, 5가 있으며 두 집합은 일치한다. 이때 집합의 크기는 3이다. 만약 첫째 줄에서 1과 3을 뽑으면, 이들 바로 밑에는 정수 3과 1이 있으므로 두 집합이 일치한다. 그러나, 이 경우에 뽑힌 정수의 개수는 최대가 아니므로 답이 될 수 없다.
입력:
첫째 줄에는 N(1≤N≤100)을 나타내는 정수 하나가 주어진다. 그 다음 줄부터는 표의 둘째 줄에 들어가는 정수들이 순서대로 한 줄에 하나씩 입력된다.
출력:
첫째 줄에 뽑힌 정수들의 개수를 출력하고, 그 다음 줄부터는 뽑힌 정수들을 작은 수부터 큰 수의 순서로 한 줄에 하나씩 출력한다.
풀이방법:
뽑힌 정수들이 이루는 집학과 뽑힌 정수들의 바로 밑의 둘째 줄에 들어있는 정수들이 이루는 집합이 일치한다는 것은 그 해당 정수들로 사이클이 이뤄진다는 것과 동일하다. 즉, 이 문제는 숫자 배열들 중에서 가장 큰 사이클을 찾으면 된다.
따라서 사이클을 찾기 위해 DFS를 사용하여 문제를 풀도록 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
from collections import defaultdict
def dfs(now,start):
visited[now] = 1
for n in numbers[now]:
if not visited[n]:
dfs(n,start)
elif visited[n] and n==start:
answer.append(n)
N = int(input())
numbers = defaultdict(list)
for i in range(1,N+1):
numbers[i].append(int(input()))
answer = []
for i in range(1,N+1):
visited = [0 for _ in range(N+1)]
dfs(i,i)
print(len(answer))
for i in range(len(answer)):
print(answer[i])
|
cs |
문제링크:
https://www.acmicpc.net/problem/2668
2668번: 숫자고르기
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절
www.acmicpc.net
'Algorithm > Python' 카테고리의 다른 글
| [BOJ] 17140. 이차원 배열과 연산 (0) | 2021.10.19 |
|---|---|
| [BOJ]2659. 십자카드 문제 (0) | 2021.10.18 |
| [BOJ] 16918. 봄버맨 (0) | 2021.10.14 |
| [BOJ] 16236. 아기 상어 (0) | 2021.10.13 |
| [BOJ] 15683. 감시 (0) | 2021.10.12 |