DSANet : Dual Self-Attention Network for Multivariate Time-Series Forecasting
ABSTRACT
Multivariate Time-Series Forecasting을 하는데 전통적인 model이나 RNN과 attention을 사용하는 모델로 수행하기에는 어려움이 있다. 따라서 이번 논문에서 DSANet을 제안하는데 이 문제를 해결했다.
global Temporal Convolution과 local Temporal Convolution을 parallel하게 사용했고, 이 과정을 거친 뒤 Self-Attention을 수행한다. 마지막으로 linear한 특징을 부여하기 위해 AR을 사용해 최종 예측값을 얻는 모델이다.
1.Introduction
multivariate time series forecasting이 연구되는 중이다.
- sensor network , road occupancy rates forecasting, financial market prediction
- 하지만 complex하고 non-linear dependencies 문제로 인해서 어려움을 겪고 있다.
- 심지어 이 dependencies는 dynamic하게 변해서 분석이 더 어렵다.
전통적인 방법(VAR, GP)등은 non-linear dependencies을 잡아내지 못해서 사용할 수 없다.
RNN 계열들은 이러한 non-linear dependencies을 잡아낼 수 있지만 long-time dependency 문제가 발생한다.
- LSTM과 GRU를 사용하거나 attention을 사용하면 이러한 문제를 해결할 수 있다.
- 하지만 현실 세계에서 흔히 발생하는 nonperiodic patterns과 dynamic-period patterns을 해결하지는 못한다.
따라서 이러한 문제를 해결하고자 dual self-attention network(DSANet)을 제안한다.
- univariate time serie들을 두 개의 평행한 parallel convolutional components에 넣는다.
- global temporal convolution , local temporal convolution
- 각 convolution에서 나온 representation을 각각 self-attention에 넣어준다.
- 이는 다른 series들 간의 dependency를 배우기 위함이다.
- 마지막으로 linear한 특징을 더해주기 위해서 autoregressive 값을 더해준다.
- univariate time serie들을 두 개의 평행한 parallel convolutional components에 넣는다.
2. Related Work
생략
3.Preliminaries
univariate time seires는 X(i) = <x1(i),x2(i),...,xT(i)>와 같이 표현을 하며 이를 multivariate로 확장하면 X=<X(1),X(2),...,X(D)>와 같다.
우리가 해결해야 할 문제는 <X1,X2,...,XT>가 주어졌을 때, XT+h를 예측하는 일이다.
- 동일하게 XT+h+k를 예측하기 위해서는 <X1+k,X2+k,...,XT+k>가 필요하다. 즉 input window size k만큼의 범위의 값을 알아야 한다.
4.Methodology
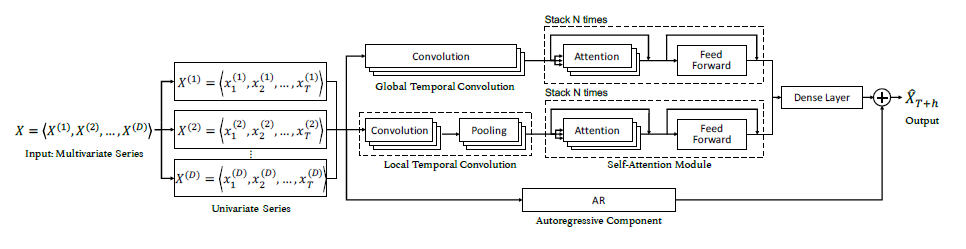
- Introduction에서 설명했던 구조를 하나씩 자세히 살펴보도록 한다.
Global Temporal Convolution
- Deep learning method인 RNN을 사용해서 temporal한 pattern을 잡곤 했지만 long term의 특징을 잡지 못했다.
- 따라서 multiple Tx1 filter를 사용하는 convolution인 global temporal convoltion(TCN)을 사용한다.
- 각 global TCN의 filter는 input matrix X를 훑으며 D 크기의 vector를 생산해낸다.(activation function은 ReLU를 사용한다.) 각 filter에서 나온 vector들을 합쳐서 output matrix HG를 만들어낸다.
- 각 filter별로 각 time seires를 표현하는 값을 얻어서 D 크기의 vector가 나온다.
- matrix의 각 행은 univariate series의 representation이라고 할 수 있다.
Local Temporal convolution
- 현재 시점으로부터 가까운 time step들이 멀리 있는 time step보다는 더 관련있을 가능성이 높다.
- 따라서 global TCN은 이 time series의 전반적인 특징을 살펴보았다면, 이번에는 local한 특징을 찾아보도록 한다. 이 과정은 parallel하게 수행된다.
- global TCN과 다른 점이라고 하면 filter size의 크기를 l로 사용하는데, l<T보다 작은 수이다.
- 따라서 각 filter별로 vector가 아닌 matrix MkL를 생성해낸다.
- 각 univariate time series의 local temporal relation을 vector representation으로 map하기 위해서 DSANet은 1-D max pooling을 사용한다.
- 따라서 최종 output인 matrix HL을 얻게 된다.
Self-Attention Module
self-attention이 feature extraction 능력이 좋기 때문에 서로 다른 series간 dependency를 포착하기 위해 사용한다.
각 univariate representation을 input으로 넣어주도록한다.
- 그러면 자기 자신을 포함해서 다른 representation간의 관계를 파악한다.
N identical layer를 stack하며, self-attention layer와 position-wise feed-forward layer를 가지고 있다.
- 일반적인 Self-Attention 구조이다.

resulting weighted representation을 결합하고 linearly projected해서 final representation ZOG를 얻게 된다.
position-wise feed-forward layer를 통과해서 최종 결과인 FG를 얻는다.
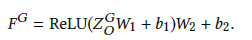
local도 똑같이 적용해서 FL를 얻는다.
Autoregressive Component
- convolution과 self-attention은 모두 non-linear한 특징을 가지기 때문에 neural network의 scale이 input에 sensitive하지 않게 되었다. 따라서 linear한 특징을 부여하기 위해서 AR을 사용한다.
Generation of Prediction
- 예측단계에서 각 self-attention에서 나온 값들을 dense layer를 통해서 결합하고 AR에서 얻은 값을 더해서 최종 예측값을 얻는다.
5.Experiments
- dataset은 지리적으로 가까운 5개의 gas station 데이터를 사용했다.
- root relative squared error(RRSE), mean absolute error(MAE), empirical correlation coefficient(CORR)를 사용해서 측정했고, hyperparameter들은 이것저것 많이 했다고 한다.

- 다음은 실험결과 중 일부인데, 32일의 데이터가 있을 때, 각 3일, 6일, 12일, 24일 뒤의 값을 예측하는 실험이다.
- 당연히 24일 뒤가 맞추기 힘드므로 값이 가장 클 것이다.
- 기존에 있던 method보다 DSANet이 가장 좋은 성능을 보였다.
Ablation Study

- model의 일부분을 하나씩 빼고 실험한 결과인데, AR이 이 모델에서 가장 큰 영향을 끼치고 있음을 알 수 있다.