Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.
3. Planning by Dynamic Programming
- Model Free : environment에 대한 정보를 가지고 있지 않을 경우
- Model Based : environment에 대한 모델이 있는 경우
- 이러한 경우에 대해서 Planning, Dynamic Programming을 사용한다.
Introduction
-
What is Dynamic Programming?
알고리즘 문제 기법에서 사용하는 DP, 동적 계획법과 같은 뜻을 가지고 있다. 복잡한 문제에 사용하는 방법으로써 문제를 여러 subproblem으로 쪼갠 뒤에 이 문제를 해결하고 합쳐가면서 풀어가는 방식이다.
- 다음과 같이 두 가지 특성을 가지는 문제에 대해서 DP를 사용하는 것이 일반적이다.
- Optimal substructure
- Optimal한 해는 subproblems들로 분해될 수 있다는 것이다.
- Overlapping subproblems
- Subproblem 들이 많이 사용되어서 이를 저장해두었다가 사용할 수 있다.
- Optimal substructure
- MDP는 위 두 가지 속성을 가지고 있으므로 DP를 사용할 수 있다.
- Bellman equation은 재귀적으로 분해가 가능하고, value function은 해를 저장하고 재사용할 수 있도록 한다.
- 다음과 같이 두 가지 특성을 가지는 문제에 대해서 DP를 사용하는 것이 일반적이다.
-
Planning by Dynamic Programming
DP는 MDP의 모든 것을 알고 있다고 가정한다. 즉 Planning 문제를 해결하는 것이다.
DP는 크게 두 가지 방법으로 나뉘게 된다.
- Prediction
- value function을 학습하는 것
- MDP, policy가 있을 때 그 policy를 따를 경우의 value function이다.
- policy evaluation 문제
- Control
- optimal 한 policy를 찾는 문제
- MDP만 있고 optimal 한 policy를 찾아야 한다.
- policy Iteration, value Iteration
- Prediction
Policy Evalutation
주어진 policy를 평가하는 문제, 이 policy를 따라 간다면 return을 얼마 받는가. 즉 value function을 찾는 문제

초기 value 값을 랜덤하게 초기화 한 후 Bellman Equation을 이용해서 다음 상태 s'를 이용해서 각각의 상태 s의 value 값을 반복적으로 업데이트 한다. 이 때 synchronous backup을 사용한다.
Example


위와 같이 계속해서 반복하다보면 정책이 수렴하는 것을 알 수 있다.
Policy Iteration
위와 같이 반복적인 업데이트를 통해서 모든 상태 s에 대해 value 값을 구할 수 있다.(Evaluate) value 값이 최대가 되는 방향으로 greedy하게 행동하면 초기에 만들었던 Random한 Policy를 개선된 Policy로 만들 수 있다.(Improve) 위와 같은 예시에서는 금방 최적의 Policy로 찾아가는 것을 알 수 있다.
따라서 일반적인 경우에는 Policy를 evaluation해서 value들을 구하고, 그 value들을 바탕으로 Policy를 improvement하는 방향으로 발전시키면 된다.
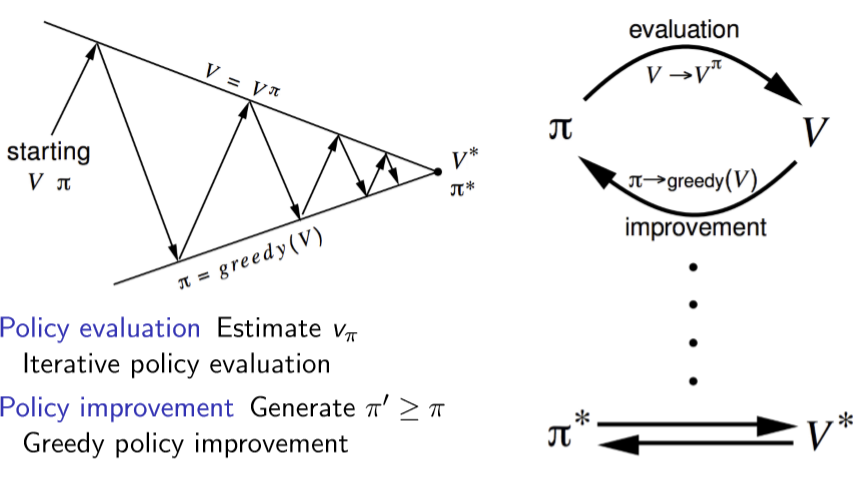
그런데 과연 greedy 하게 정책을 개선시키는 것이 성능을 항상 좋게 만들까?

다음과 같은 이유들로 항상 그렇다고 하며, 수렴을 하는 포인트는 optimal 하다고 한다.
-
Modified Policy Iteration
하지만 꼭 수렴할 때까지 계속해서 반복해서 진행해야 하는가? 에 대한 의문을 가질 수 있다. 실제로 무한히 반복해서 수렴할 때까지 진행을 하지 않고, k번을 반복해서 그 점을 사용해도 충분히 합리적으로 사용할 수 있다고 한다.
Value Iteration
Value Iteration은 Policy Iteration과는 다르게 Bellman Optimal Equation을 이용하는 것이다.
- Deterministic Value Iteration
- subproblem의 solution을 알면 Bellman Optimal Equation을 이용해서 s에서의 solution을 알 수 있다.
- 이러한 반복을 계속해서 한다.
- 아래는 위의 Grid world의 Value Iteration을 적용한 것이다.

- 반복해서 진행하면 세번째 iteration에서 converge 하는 것을 알 수 있다.
Summary of DP Algorithms
| Problem | Bellman Equation | Algorithm |
|---|---|---|
| Prediction | Bellman Expectation Equation | Iterative Policy Evaluation |
| Control | Bellman Expectation Equation + Greedy Policy Improvement |
Policy Iteration |
| Control | Bellman Optimality Equation | Value Iteration |
'Book > Reinforcement Learning' 카테고리의 다른 글
| [RL]Lecture 5. Model-Free Control (0) | 2020.02.12 |
|---|---|
| [RL]Lecture 4. Model-Free Prediction (0) | 2020.02.05 |
| [RL]Lecture 2. Markov Decision Processes (0) | 2020.01.22 |
| [RL] Lecture 1. Introduction to Reinforcement Learning (0) | 2020.01.15 |
| [RL]ch 0. Intro (0) | 2020.01.15 |