*Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.
Markov Decision Process을 지난 강의에서 배웠던 내용으로 설명하면, 강화학습을 위해 환경을 완전하게 알고 있는 것을 의미한다. 즉 full observable해야 한다. 이러한 이유로 RL의 거의 모든 문제는 MDP로 설계가 되어 있고, MDP하지 않다면 MDP하도록 조건을 더 추가시켜줘야 한다.
Markov Property
이전 강의에서 잠시 다뤘던 내용이다. "Markov하다" 라는 것은 다음 상태는 과거 상태에는 독립적이고 현재 상태에만 종속을 한다는 것이다. 즉 다음과 같다.
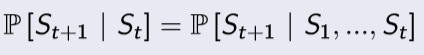
예시로 설명하면 다음과 같다. 현재 내가 장기(체스)를 두고 있다고 하자. 그러면 지금 현재 기물들이 어떻게 놓여져 있는지가 다음 수를 두는 것에 영향을 줄 뿐, 이전에 어떻게 움직였는지는 전혀 다음 수에 도움이 되지 않는다.
State Transition Matrix
Markov를 설명하기 위해 도움이 되는 정의 중 하나이다. state transition probability는 Markov한 state s에서 다음 상태 s'으로 이동할 확률을 뜻하고, Matrix는 이러한 확률을 행렬꼴로 모아둔 것이다.


Markov Process
앞으로 다룰 Markov 대한 성질들의 가장 기본이 되는 과정이다. memoryless random process라고 하는데, 이는 Markov의 특징을 말하는 것이다. Markov Process는 <S,P>로 정의되고, S는 state들의 집합, P는 state transition probability matrix이다. 다음은 아기가 잠에 드는 과정을 도식화한 것이다.


여기서 각 행동은 다 타원형으로 표시되어 있고, '잔다' 라는 상태만 네모로 표시되어 있는데 이는 terminate state, 종료 상태를 의미한다. 각 행동으로 이동하는 화살표에 확률이 써져 있는데, 아직은 모든 상태는 확률에 의해서만 바뀐다. 즉, '눕는다.' 라는 상태에서는 70% 확률로 논다. 라는 상태로 이동하고, 30%으로 확률로 잠에 들기 시작하는 상태로 이동하는 것이다.
상태를 이동하는 상황이 여러가지 있는데 이들을 episodes라고 부른다.
Markov Reward Process
Markov Process에 Reward function이 추가된 개념으로 <S,P,R,r>와 같으며 R은 reward function으로 Rs=E[Rt+1|St=s]이고, r 은 감쇠인자로써, 0과 1 사이의 값을 가진다. 이 단계에서 새로 정의되는 개념들이 있어 이를 정리하고 진행한다.

Return
return Gt는 t 시간이 지난 뒤에 얻은 총 보상을 의미한다.
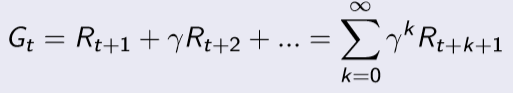
- Why discount? 감쇠인자를 사용하는 이유는 무엇일까?
- 수학적으로 편리하다. 감쇠 인자를 0과 1 사이의 값으로 설정을 했기 때문에 return 값이 무한히 커지는 것을 막을 수 있다. 즉 bounded하게 만들 수 있다.
- 사람이 선호하기 때문이다.
- 만약 누군가 당신에게 지금 커피를 사줄지? 아님 10달 뒤에 커피를 사줄지 물어볼 수 있다.
- 대부분 지금 사달라고 할 것이다.
- 만약 누군가 당신에게 지금 커피를 사줄지? 아님 10달 뒤에 커피를 사줄지 물어볼 수 있다.
- 불확실성을 표현하기 위해서
- 위의 예시로 생각하보면 지금 사달라고 선택을 하는 이유가 10달 뒤에 진짜 커피를 사줄지는 불확실했기 때문일 것이다.
Value Function
value function은 현재 상태 s로 부터 시작했을 때 return의 기댓값을 의미한다.
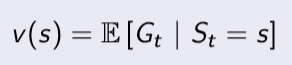
지금까지 예시에서 감쇠인자 값을 0이라 가정했을 때, 다음과 같이 value function 값이 구해진다.
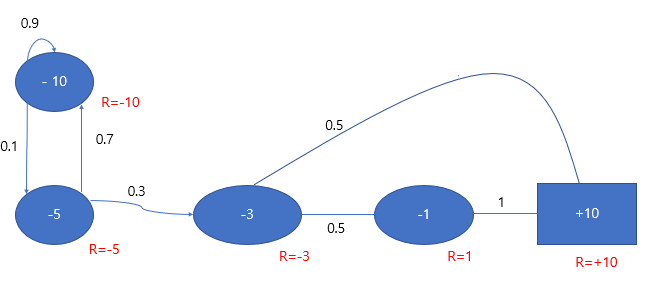
지금은 state들이 단순해서 충분히 손으로도 계산을 할 수 있지만 더 많은 state들이 복잡하게 연결된다면 손으로 하는 것은 어렵게 될 것이다. 따라서 이를 위해 Bellman Equation이라는 것을 사용한다.
Bellman Equation
value function을 다음과 같이 표현할 수 있다.
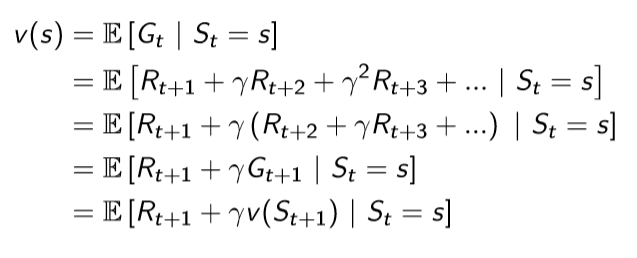
Bellman Equation으로 value function을 그림으로 표현하면 다음과 같다. 현재 상태의 value function은 현재 보상을 받은 뒤(Rs)에 다음 상태들의 value function 합(sigma Pss'v(s'))에 감쇠 인자를 곱한 값을 얻는다는 것이다.

따라서 이와 같이 value function으로만 구성된 식을 matrix form으로 변환한다면 역행렬을 통해서 한번에 구할 수 있게 된다.
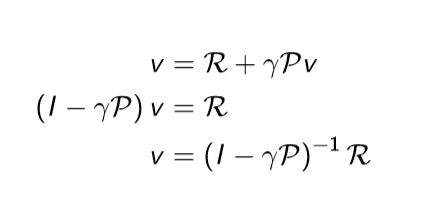
하지만 이 연산은 O(n^3)에 해당하는 복잡도를 가지고 있다. 따라서 작은 MRP에서만 계산이 가능하고, 큰 경우는 DP, Monte-Carlo 방법등으로 구하게 된다.
Markov Decision Process
Markov Reward Process에서 action이 추가된 단계이다. <S,A,P,R,r>와 같이 정의 하며 A는 action들의 집합을 의미한다.
또한 action이 추가되었기 때문에 상태천이행렬 P와, reward function R에 a에 관한 식이 들어가게 되었다. 따라서 슬라이드에서 소개한 내용에 action을 추가하면 다음과 같다.

그리고 Action이 생김에 따라서 몇 가지 용어를 정의해야 한다.
Policy
정책 π 는 현재 주어진 상태에서 action a를 수행할 분포를 의미한다.
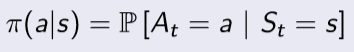
따라서 정책은 agent 행동을 정의한다고 할 수 있다. 그리고 이 정책을 이용해서 상태천이행렬 P와 reward function R을 다음과 같이 다시 정의할 수 있다.
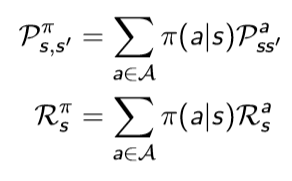
Value Function
- state-value function
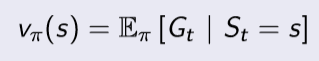
state value function은 현재 상태 s가 주어졌고, 정책을 따른다고 했을 때 얻을 수 있는 return의 기댓값을 의미한다.
- action-value function

action value function은 현재 상태가 s이고, action a를 한다. 그리고 정책을 따른다고 했을 때, 얻을 수 있는 return의 기댓값을 의미한다.
Bellman Expectation Equation
위에서 정의했던 state value function과 action value function을 Bellman equation을 사용하기 위해서 Immediate reward와 future reward 형태로 분해할 수 있게 된다.


하지만 위 식으로는 실제로 구현을 하는 것이 힘들기 때문에 직접 구현을 위해 조금 더 명백한 형태로 변형이 필요하게 됩니다.

위 그림에서 흰색 원은 state를 의미하고, 검은색 원은 action을 의미합니다. 위 그림을 해석해 보면 현재 상태 s에서 가능한 action들은 2개가 있는 것입니다.(실제로는 더 많은 검은색 점이 있을 수 있습니다.) 그러면 agent가 선택한 당시의 정책에 따라 action을 할 확률이 정해질 것이고, 그 때마다 action-value function을 구할 수 있게 됩니다.
따라서 위 그림으로 보아 우리는 현재 state s에서의 state value function을 구하기 위해서 각 action을 할 확률(정책)과 그 action에서 발생하는 value state function을 곱한 것들의 합으로 표현을 할 수 있게 됩니다.
즉 다음과 같이 식을 얻을 수 있습니다.
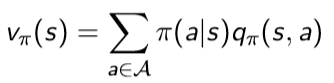
하지만 아직 이 형태로는 현재 state value function과 다음 state value function과의 관계를 알 수 없습니다. 그러므로 action value function에 대해서 식을 전개해보도록 하겠습니다.

state s에서 action a를 했을 때의 그 action에 대한 value는 두 가지로 나뉘게 됩니다. state s에서 action a를 했을 때의 reward와 그 다음 state의 value function입니다. 그런데 이 중 다음 state value function은 다음 시점의 value function이므로 감쇠 인자를 적용시켜줘야 합니다. 또한 상태가 변한 것이므로 상태 전이 확률도 적용시켜줘야 합니다. 따라서 다음과 같이 식을 구성할 수 있습니다.

따라서 위 두 내용을 모두 한 번에 합치면 다음과 같이 됩니다.

지금까지 state value function을 설명하기 위해 전개를 한 것처럼 이를 action value function을 설명하기 위해 전개를 진행하면 다음과 같이 됨을 알 수 있습니다.

이제 식을 state, action value function 하나씩으로만 표현을 할 수 있기 때문에 이전에 matrix form으로 변경해서 구했떤 것처럼 구할 수 있게 된다.

Bellman Optimal Equation
강화학습은 기본적으로 최대의 보상을 얻는 정책을 찾는 것을 목표로 하고 있기 때문에 얻을 수 있는 기댓값보다는 최대 보상을 얻을 수 있는 것이 더 중요합니다. 따라서 앞서 정의했던 value function들을 다음과 같이 정의할 수 있습니다.


위의 식으로 optimal한 value function을 구할 수 있다면 주어진 state에서 value가 가장 높은 action을 선택할 수 있고, 이를 통해서 optimal한 정책을 구할 수 있게 됩니다. optimal한 값을 항상 얻도록 만들어야 하므로 다음과 같이 정책을 수식을 적을 수 있습니다.

앞서 Expectation Equation에서 진행했던 것처럼 Optimal도 진행을 할 수 있고 다음과 같이 얻을 수 있다.
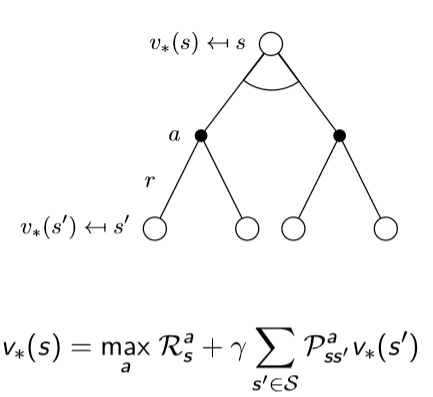
하지만 Bellman Optimality Equation은 max 연산때문에 non-linear하다. 그렇기 때문에 일반화된 해법을 제공할 수는 없고, 이를 위한 여러가지 다른 방법들을 제시한다.
- Value Iteration
- Policy Iteration
- Q-learning
- Sarsa
'Book > Reinforcement Learning' 카테고리의 다른 글
| [RL]Lecture 5. Model-Free Control (0) | 2020.02.12 |
|---|---|
| [RL]Lecture 4. Model-Free Prediction (0) | 2020.02.05 |
| [RL]Lecture 3. Planning by Dynamic Programming (1) | 2020.01.29 |
| [RL] Lecture 1. Introduction to Reinforcement Learning (0) | 2020.01.15 |
| [RL]ch 0. Intro (0) | 2020.01.15 |