CodeDrive

2.1 Introduction

이전 장에서는 확률이 어떻게 머신 러닝에서 사용될 수 있는지 살펴보았다면, 2장에서는 더 자세한 확률 이론에 대해 알아본다. 확률에 대한 기술적인 논의를 하기 전에, "확률이란 무엇인가?"라는 질문에 먼저 답해보도록 한다. 쉽게 생각할 수 있는 주제로 '동전을 던졌을 때, 앞면이 나올 확률은 0.5'라는 것은 다들 알 것이다. 사실 확률에 대한 해석은 크게 2가지가 가능하다.

1. Frequentist

• 빈도주의적인 해석으로써 장기간에 걸쳐 발생 빈도를 의미한다. 즉, 동전을 수없이 많이 던져서 앞면이 나올 확률이 0.5가 나온다는 것을 알 수 있다는 것이다.

2. Bayesian

• 베이지안 해석으로 확률은 어떤 것에 대한 불확실성을 수량화하는 것이며, 반복되는 시도보다는 기본적으로 정봐와 연관된 것이다. 즉, 베이지안적 시각으로 보면, 다음 동전 던지기 때에 앞면과 뒷면이 나올 확률은 동일하다는 것이다.

베이지안식 해석의 큰 장점은 장기간의 빈도를 가지지 않는 사건에 대한 불확실성을 모형화하는 것에 사용할 수 있다는 것이다. 따라서 이 책에서는 베이지안식 해석을 채택하여 설명하도록 한다.

2.2 A brief review of probability theory

이 절에서는 확률 이론에 대한 기초 개념을 간단히 리뷰하도록 한다. 따라서 이미 확률 이론에 대해 익숙한 사람이라면 이 절을 생략해도 무관하다.

2.2.1 Discrete random variables

p(A)는 event A가 발생할 확률을 의미한다. 예를 들어, A는 "내일 비가 올 확률"가 될 수 있다. 0<= p(A) <=1 이어야 하며, p(A)=0은 사건이 절대 발생하지 않는다는 것을 의미하고, p(A)=1은 사건이 반드시 발생한다는 것을 의미한다.
이산 확률 변수 X를 정의해서 이항 사건에 대한 개념을 확장할 수 있으며, X는 유한 집합이나 가산 무한 집합으로부터 어떠한 값도 가질 수 있다. X=x의 확률은 p(X=x)로 나타내고, 간단히 p(x)라고 나타낸다. 여기서 p()는 확률 질량 함수 또는 pmf이다.p(x)도 0과 1 사이의 값을 가지며, 총합은 1이 된다는 조건을 만족한다. 위 그림은 유한한 상태 공간에서 정의된 두 개의 pmf며, 왼쪽은 균등 분포를 가지고 있으며, 오른쪽은 퇴화 분포에 해당하며, X가 항상 1과 같다는 것을 표현한다.

2.2.2 Fundamental rules

생략

2.2.3 Bayes rule

조건부 확률의 곱, 합 법칙을 통합하면 Bayes rule을 도출 할 수 있으며, 이를 Bayes Theorem이라고 부른다.

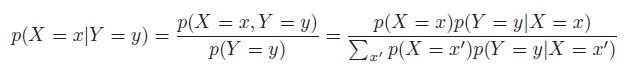
2.2.3.1 Example: medical diagnosis

베이즈 법칙을 사용하는 예로 의학적 진단 문제를 생각해보자. 당신은 40대 여성이라고 가정하고, 유방조열술로 유방암에 대한 의학 검진을 받기로 했다. 검사가 양성일 때, 실제로 암일 확률은 얼마일까?
이 확률을 구하기 위해서는 우선 검사가 얼마나 신뢰성이 있는지 알아야 한다. 검사가 80%의 정확성을 가지고 있을 경우 당신이 암이라면 0.8의 확률로 양성이 나타날 것이다. 즉, 다음과 같다.

p(x=1|y=1) = 0.8

여기서 x=1은 유방조영술이 양성인 사건을 의미하고, y=1은 유방암인 경우의 사건이다. 대부분의 사람들이 이런 경우 80%가 암이라고 결론을 내린다. 하지만 이것은 False다! 이러한 결론은 유방암을 가지고 있는 사전 확률을 무시한 것이다. 다행히도 암을 가질 확률은 매우 낮다.

p(y=1) = 0.004

사전 확률을 무시하는 것을 기저율 에러(base rate fallacy)라고 한다. 또한 테스트가 거짓 양성 또는 거짓 정보일 케이스인 경우도 고려해야 한다. 불행하게도 거짓 양성인 가능성은 높다.

p(x=1|y=0) = 0.1

베이즈 법칙을 사용해 세 개의 조건을 모두 결합하면 다음과 같이 정확한 답을 계산할 수 있다.

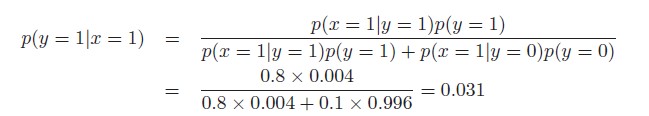
즉, 검사가 양성이라면 실제 유방암일 확률은 대략 3%에 해당한다.

2.2.4 Independence and conditional independence

X와 Y의 결합 확률을 곱으로 표현할 수 있다면 무조건적인 독립, 또는 marginally 독립이라고 하며, X⊥Y로 표현한다. 즉, 다음과 같다.

일반적으로 결합 확률이 marginal의 곱이면 변수 집합이 상호 독립적이라고 한다.
대부분의 변수는 다른 변수에게 영향을 주는 경우가 많기 때문에 무조건적인 독립은 매우 드물다. 하지만 이런 영향은 직접적이라기보다는 다른 변수에 의해 중재된다. 그러므로 조건부 결합 확률이 조건부 주변의 곱으로 표현될 수 있는 경우에만 "Z가 주어졌을 때 X와 Y는 조건부 독립이다" 라고 한다.

2.2.5 Continuous random variables

지금까지는 불확실한 이산량에 대한 추정만을 다뤘으며, 이번 절에서는 어떻게 확률을 확장해야 하는지 알아본다.
X를 불확실한 연속량으로 가정한다면, X가 a이상 b이하일 확률은 다음과 같이 계산한다.

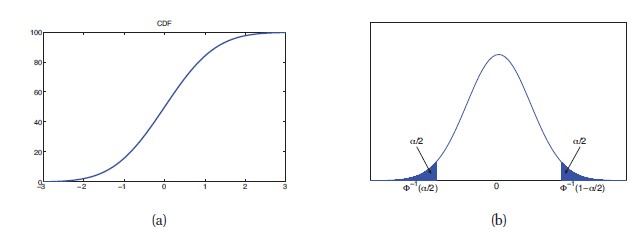
위와 같이 확률을 계산하는 것을 함수 형태로 정의하고, 이것을 X의 누적 분포 함수(cumulative distribution function) 혹은 cdf라고 정의한다. 이는 그림 (a)에 해당하고, 표기법을 사용하면 다음과 같다.

이제 도함수를 정의하고, 이것을 확률 밀도 함수(probability density function) 혹은 pdf라고 한다. 이는 그림 (b)에 해당한다. 표기법을 사용하면 다음과 같다.

2.2.6 Quantiles

cdf F가 단조 증가 함수이기 때문에 역함수를 가지고 있다. 이를 F^-1라고 하고, F의 분위수(quantile)라고 부른다. F^-1(0.5)는 중앙값이고, F^-1(0.25), F^-1(0.75)는 각각 하위 및 상위 사분위수다.

2.2.7 Meana and variance

분포를 설명할 때 가장 익숙한 속성은 평균 또는 기댓값이며, μ와 같이 표기한다. 분산은 분포의 '흩어진 정도'를 측정하는 것이며 σ2로 표기한다.

2.3 Some common discrete distributions

보편적으로 사용되는 이산 상태 공간에서 정의된 모수적 분포들에 해당한다. 자세하게 설명하지 않고, 분포의 종류들만 나열하도록 한다.

1. The binomial and Bernoulli distribuions
2. The multinomial and multinoulli distributions
3. The Poisson distribution
4. The empirical distribution

2.4 Some common continuous distributions

2.3절과 같이 분포들에 대해 나열만 하도록 한다.

1. Gaussian distribution
2. Degenerate pdf
3. The Laplace distribution
4. The gamma distribution
5. The beta distribution
6. Pareto distribution

케빈 머피의 Machine Learning 책을 보고 정리한 내용들입니다.

1.1 Machine Learning: what and why?

현재 우리는 빅데이터 시대에 살고 있으며, 수많은 양의 정보들을 마주하고 있다. 이러한 데이터들을 분석하기 위해 자동화된 데이터 분석 기법이 필요하게 되었고, 머신 러닝이 이러한 역할을 수행할 수 있다. 머신 러닝은 데이터의 패턴을 자동으로 인지하고, 다뤄지지 않은 패턴을 사용해 미래의 데이터를 예상하거나 불확실성 아래서 여러 종류의 결정을 선택하는 방법이다.

1.1.1 Types of machine learning

머신 러닝은 보통 두 개의 타입으로 구분할 수 있다.

1. Predictive, supervised learning
   • 레이블이 있는 입출력의 쌍이 주어졌을 때, 입력 x로 출력 y를 매핑하는 함수를 학습하는 것이 목표
   • 입력 x는 D차원 벡터로서 특징(feature), 속성(attribute), 공변량(covariance)라고 한다.
   • 출력 y는 한정된 값을 가지는 범주형 변수, 실수 값을 가지는 스칼라 변수가 있을 수 있다.
     • y가 범주형인 경우 분류(classification), 실수인 경우는 회귀(regression)이라고 한다.
2. Descriptive, unsupervised learning
   • 해당 방법에서는 입력만이 주어지고, 데이터 내의 흥미있는 패턴(interesting pattern)을 찾는 것이다.
   • 찾고자 하는 패턴이 주어지지 않기 때문에, 정의가 불분명하고, 에러를 측정할 수 있는 명확한 방법이 없다.
3. Reinforcement learning
   • 보상(reward)이 주어질 때 동작이나 행동을 배울 때 유용하다.
   • RL에 대해서는 이 책에서 자세히 다루지 않도록 한다.

1.2 Supervised learning

1.2.1 Classification

Classification의 목적은 입력 x로부터 출력 y를 매핑하는 것을 학습하는 것으로, y는 1~C의 값을 가지며, C는 class의 갯수를 의미한다. C=2인 경우에는 binary classification이라 하고, C > 2는 multiclass classification이라고 한다.
훈련 데이터에 대해서 학습을 하고 예측을 하는 것을 쉽기 때문에 classification의 주요 목적은 전에 보지 못했던 데이터들에 대해서도 답을 정확하게 예측하는 것(Generalization)이다.

1.2.1.2 The need for probabilistic predictions
주어진 입력 벡터 x와 훈련 집합 D에 대해 가능한 레이블들의 확률 분포를 나타낸다. 일반적으로 이 것은 길이가 C로 나타난다. 훈련 집합 D 뿐만 아니라 테스트 입력 x에 대한 조건부 확률이라는 것을 명시적으로 나타내기 위해 표기법에서 조건식 기호 | 의 오른쪽에 D와 x를 둔다.

확률적인 결과가 주어진다면, 다음의 식을 사용하여 레이블 값이 참인 경우에 대해 최선의 추측을 계산할 수 있다.

이 값은 가장 확률이 높은 클래스 레이블이고, 최대 사후 확률(MAP estimate) 로 알려져 있다. 해당 내용은 5.7에서 수학적인 검증을 한다.
다음과 같은 분야에서 실제로 응용되고 있다.

1. 문서 분류와 이메일 스팸 필터링
2. 꽃 분류
3. 이미지 분류와 글씨 인식
4. 얼굴 검출과 인식

1.2.2 Regression

Regression은 결과 변수가 연속적이라는 것을 제외하고 분류와 같다. 다음 그림은 단순한 예시를 보여준다.

다음은 실생활에 존재하는 Regression 문제의 예다.

• 현재 시장 상황과 다른 가능한 정보를 통해 다음 날의 주식 시장을 예측하는 것
• YouTube를 보는 사용자의 나이 예측
• 날씨 데이터와 시간, 문의 센서를 통해 건물 안의 온도를 예측하는 것

1.3 Unsupervised learning

Supervised learning과는 다르게 각 입력에 대해 기대되는 출력이 주어지지 않는다. 대신 작업을 확률 밀도 추정의 하나로 공식화한다. 즉, p(x|theta) 형태의 모형을 설계하는 것이 목표다. 이 말은 Unsupervised learning은 비조건적인 밀도 추정 문제에 해당한다.

1.3.1 Discovering clusters

Unsupervised learning의 기본이 되는 예제로 데이터를 그룹으로 clustering하는 문제다. 아래 그림은 210명의 키와 몸무게 대한 데이터들이다. 여러 개의 클러스터나 하위 그룹이 있는 것으로 보인다. K가 클러스터의 숫자를 의미한다고 하면, 첫 번째 목표는 p(K|D)를 예측하는 것이다. Supervised learning에서는 남자/여자와 같은 클래스가 있지만 Unsupervised learning은 클러스터의 갯수를 자유롭게 설정할 수 있다.
두 번째 목표는 각 데이터가 어떤 클러스터에 속하는지를 추정하는 것이다.(b)는 K=2일 때의 결과에 해당한다.

이 책에서는 model based clustering에 초점을 맞춘다. 모형 기반 클러스터링은 객관적인 방법으로 여러 모형을 비교할 수 있고, 여러 모형을 더 큰 시스템으로 조합할 수 있다.

클러스터링의 실제 응용은 다음과 같다.

• 천문학에서 천제 물리학의 측정값을 클러스터링하여 새로운 타입의 별을 발견할 수 있다.
• e-커머스에서 구입 내역과 웹 서핑을 분석하여 사용자들을 분석할 수 있고, 각 그룹에 타켓팅한 광고를 설정할 수 있다.

1.3.2 Discovering latent factors

고차원의 데이터를 처리할 때에는 데이터의 'essence'을 가지고 있는 작은 차원의 부분 공간으로 사영시키는 것이 유용하다.이것을 차원 축소라고 부른다. 아래 그림은 간단한 예시로, 3차원의 데이터를 2차원 평면으로 투영한 것이다.

2차원 데이터로 투영한 (b)는 유사한 위치에 놓여 있는 것을 보아 결과가 좋게 나왔지만, 1차원으로 축소한 (a)의 빨간 선은 결과가 좋지 못하다. (해당 내용은 12장에서 더 자세히 다룬다.)
낮은 차원의 표현은 다른 통계 모형의 입력으로 사용하면 좀 더 예측 정확도가 높아진다. 이는 불필요한 특징을 거르기 때문이다. 차원 축소를 위한 가장 일반적인 접근은 주성분분석(Principal Componenet Analysis, PCA) 이다. 이는 linear regression의 비지도 버전과 같다. 고차원 응답 y를 관찰하지만, 저차원의 '원인' z는 발견하지 못한다. 이 모델은 z -> y 형태를 가지고 , 화살표를 뒤집어서 관찰된 고차원 y를 통해 잠재된 차원 z를 추정해야 한다.

1.3.3 Discovering graph structure

상관관계가 있는 변수를 측정하고, 가장 관련이 있는 것을 발견하려는 때가 있다. 이러한 구조는 그래프로 표현할 수 있다. 노드는 변수를 표현하고, 엣지는 변수 사이의 의존 관계를 표현한다.

1.3.4 Matrix completion

데이터가 손실되는 경우가 있다. 즉, 변수의 값을 모르는 경우가 발생할 수 있다. 따라서 이렇게 손실된 데이터에 타당한 값을 추정하는 것이며, 이것을 매트릭스 완성이라고 한다.