Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.
5. Model Free Control
- Model Free : MDP에 대한 정보가 없는 경우, 즉 environment에 대한 정보를 가지고 있지 않다.
- Control : value function을 최적화 하는 것, 즉 최적의 정책을 찾는 것
Model Free Control에서는 다양한 예제들이 있으며, 주로 다음 특징을 가지는 문제들을 해결한다,
- MDP를 모르지만, 경험을 sampling 할 수 있다.
- MDP는 알지만, sample들을 제외하고는 사용하기에는 너무 크다.
On Policy & Off Policy
- On Policy learning
- "Learn on the job"
- 학습하는 policy와 행동하는 policy가 같은 경우
- ex)Sarsa
- Off Policy learning
- "Look over someone's shoulder"
- 학습하는 policy와 행동하는 policy가 반드시 같지 않아도 된다.
- ex)Q-learning
On-Policy Monte-Carlo Control
-
Generalised Policy Iteration
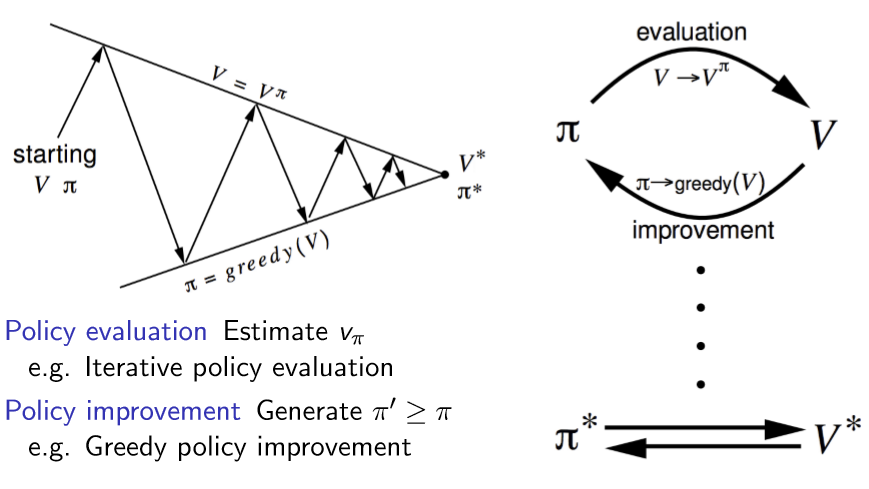
- 3장에서 배웠던 내용으로 최적의 정책을 찾는 문제를 해결하기 위한 일반적인 방법론이다.
- 임의의 정책으로 시작하여 value function을 추정하는 단계를 거친다.
- 추정한 value를 바탕으로 정책을 발전시킨다.
- 다시 맨처음으로 돌아간다.
- 이는 EM 알고리즘과 같은 형태를 가지고 있다.
- 따라서 Policy evaluation을 E단계, Policy improvement를 M 단계라 지칭한다.
- 3장에서 배웠던 내용으로 최적의 정책을 찾는 문제를 해결하기 위한 일반적인 방법론이다.
-
4장에서 value function을 estimate 하는 방법들에 대해서 배웠는데 이를 E 단계에 적용해보도록 한다.
- 하지만 그대로 적용한다면 다음과 같은 3가지 문제가 발생하게 된다.
- Value funcion의 model-based
- Local optimum
- Inefficiency of policy evaluation
- 하지만 그대로 적용한다면 다음과 같은 3가지 문제가 발생하게 된다.
1. Model-based

MC로 E단계를 수행하게 된다면 state value function을 사용해야 한다. 하지만 value function을 사용하면 M단계를 진행할 때 문제가 발생하게 된다. MC를 사용했던 이유가 Model-Free이기 때문이지만 value function으로 policy를 improve하려면 MDP의 model을 알아야 한다.

즉 위와 같이 reward와 state transition probaility를 알아야 한다. 즉 Model-based이어야 한다는 것이다.
따라서 이를 해결하기 위해서 value function을 action value function으로 바꾸게 되면 Model-Free 성질을 만족할 수 있다.

- return이 아닌 agent가 episode마다 random하게 움직이며 얻은 reward들 그리고 state transition prob.를 통해서 action-value function을 계산할 수 있다.
2. Local optimum

그러면 이제 Policy evaluation에서 value function을 action value function으로 바꾼다면 On policy MC를 사용할 수 있는 것일까? 다음 예시를 살펴보도록 한다.

-
두 개의 문이 내 앞에 있다.
-
처음 왼쪽 문을 열었고, reward 0을 받았다.
- V(left) = 0
-
두번째에는 오른쪽 문을 열었고, reward 1을 받았다.
- V(right) = +1
-
세번째에 오른쪽 문을 열었고, reward 3을 받았다.
- V(right) = +2
-
네번째에 오른쪽 문을 열었고, reward 2를 받았다.
- V(right) = +2
-
그러면 지금까지 상황을 보았을 때 어느 문을 여는 것이 최선의 선택일까?
- 아마도 이 네가지 상황으로만 본다면 오른쪽 문을 여는 것이 최선의 선택으로 보인다. 하지만 다음에 왼쪽 문을 열었을 때 reward를 100을 받을 수도 있는 것이다. 즉 지금 탐험과 탐사 trade-off에 빠지게 된 상황이다.
-
exploration(탐험) : environment에서 더 많은 정보를 알아내고자 하는 방법으로, 모든 행동을 할 때 일정 확률로 다른 곳으로 이동한다.
-
exploitation(탐사) : 알고 있는 정보를 바탕으로 보상을 최대화하고자 하는 것이다.
-
즉 지금 greedy 하게 improve 하는 것은 탐사에 빠지게 되는 것이다. 따라서 탐험을 어느정도 보장함으로써 model을 모르는 상황에서 더 좋은 성능을 낼 수 있을 것이다.
따라서 policy를 최적화 할 때 다음과 같이 일정한 확률을 부여해서 정하도록 한다.

3. Inefficiency of policy evaluation
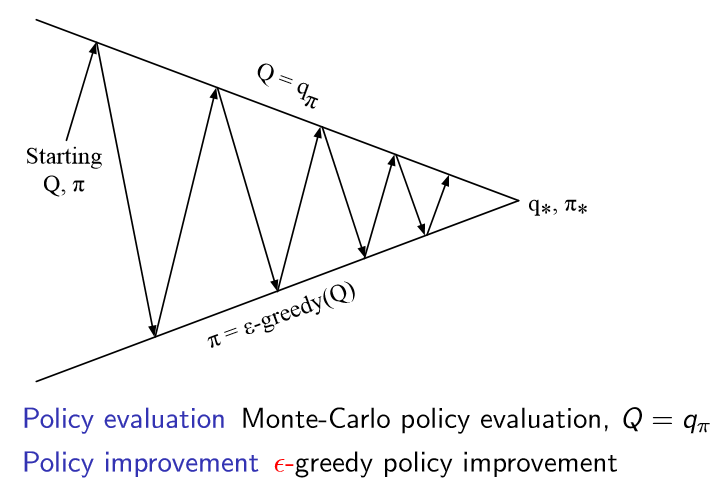
하지만 MC 방법의 경우에 모든 episode들을 다 마친 후에 evaluation을 하면 너무 오랜 시간이 걸린다는 단점이 존재하게 된다. 따라서 이를 줄이기 위해서 매 episode들이 끝난 후에 policy evaluation을 수행하는 것으로 바꾸도록 한다.
즉 최종적인 On-Policy Monte-Carlo Control은 다음과 같다.

On- Policy Temporal-Difference Learning
TD가 MC보다 적은 variance를 가지고 online으로 학습가능하며, Incomplete sequence라는 장점들을 가지고 있기 때문에 control 문제에 적용해볼 수 있다.
Prediction에서 TD는 다음과 같이 표현을 했었다.
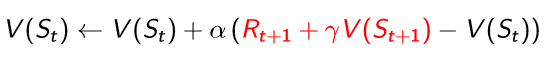
MC와 같은 이유로 value function을 사용할 수 없으므로 해당되는 부분들을 action value function으로 수정하도록 하자. 따라서 S에서 A 행동을 하면 보상 R을 받고 S'이라는 상태로 이동한다. 이 상태 S'에서 A'이라는 임의의 행동을 할 때의 action value function 값이 필요한 것이므로 다음과 같이 표현할 수 있다.
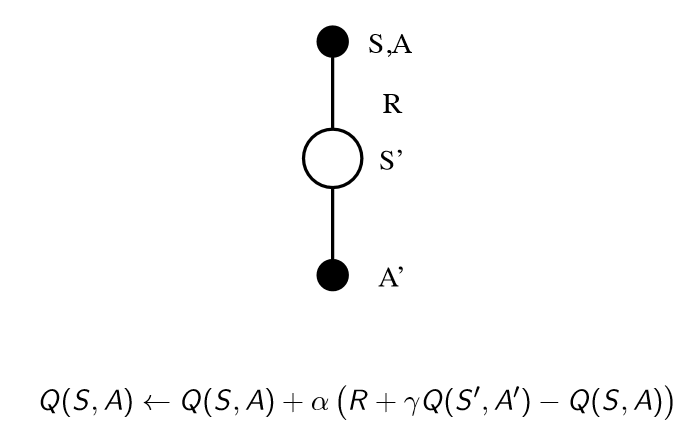
따라서 이를 앞부터 철자를 따서 Sarsa라고 부른다. Policy evaluation 부분에 MC 대신에 sarsa를 적용하면 다음과 같다.


n-step Sarsa
Sarsa가 애초에 TD의 개념에서 나온 것이므로 TD(λ)와 마찬가지로 Sarsa(λ)로 사용할 수 있다.
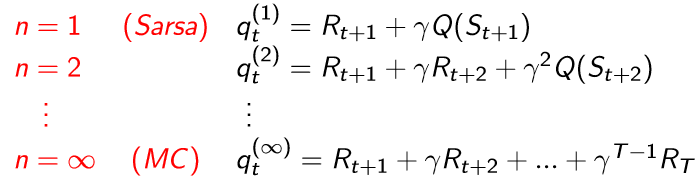
-
forward view Sarsa(λ)
-
MC와 TD의 절충안이 n-step인 것처럼, 여러 개의 n-step을 선택하여 이의 평균을 취하면 각 n-step의 장점을 모두 가질 수 있게 된다. 이 때, 단순히 산술평균을 사용하는 것이 아니라 λ라는 weight를 이용해서 가중 평균을 취하도록하고 이를 Forward-view라고 한다.
-
episode가 모두 끝나야 계산이 가능하다. 따라서 TD의 장점을 많이 잃게 된다.

-
-
backward view sarsa(λ)
-
이제는 다시 forward-view TD(λ)에서 time-step마다 update할 수 있는 방법을 알아본다. 여기서 eligibility trace라는 개념이 나오게 된다. 이는 과거에 방문했던 state 중에서 현재 얻게 되는 reward에 영향을 주는 state를 판단해, 현재 얻게 되는 reward를 해당 state에 나누는 것이다.
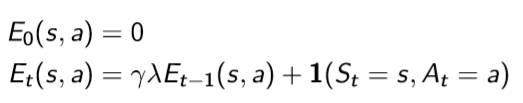
-
Off- Policy learning
자신의 policy가 아니라 다른 사람의 policy를 통해서 학습을 하는 것이다. 이는 다음과 같은 관점으로 인해 중요하다.
- 다른 agent를 관찰하는 것으로부터 배운다.
- 다른 사람의 policy를(행동을) 따라 하는 것이 아닌, 경험만을 받아 학습해서 새로운 행동을 한다.
- On policy의 경우에는 경험을 통해 policy를 업데이트를 했다면 사용한 경험은 버린다. 하지만 off policy는 이를 버리지 않고 재사용한다.
- 탐험적인 행동을 하면서 최적의 policy를 찾을 수 있다.
- 한 policy를 따르면서 여러 개의 policy를 학습할 수 있다.
Importance Sampling

X는 확률분포 P상에서 sampling 되는 것이고, Q는 P와 다른 확률분포를 의미한다. f(X)는 모든 함수를 넣을 수 있다. (f(X)=x, f(X)=3x...) 따라서 P를 따를 때의 f(X)의 기댓값을 구하고 싶은 것이다. 그런데 이를 이용해서 Q를 사용했을 때의 기댓값을 구하고 싶은 것이다.
이는 확률 분포 P와 Q의 비율을 곱해서 얻을 수 있는 것이다. 이를 Monte-Carlo에 적용해보자.
-
Importance Sampling for Off-Policy Monte-Carlo
-
Monte Carlo를 수행할 때, 지나온 모든 행동들에 대해서 비율을 곱해준다.
-
하지만 µ가 0이면 되면 사용할 수 없고, variance가 엄청 크기 때문에 사실상 사용할 수 없다.
-
-
Importance Sampling for Off-Policy TD
- 따라서 MC의 단점을 보완하기 위해서 TD를 사용하도록 한다.
Q-learning
Importance learning을 하지 않으면서 off-policy를 사용하기 위한 방법이다. 다음 행동은 behavior policy로 고르고, 다음 state S'에서 action A'은 target policy를 통해서 선택하는 것이다. 즉 다음과 같이 q-function이 업데이트가 된다.
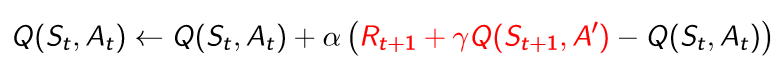
Off-policy control with Q-learning
Q-learning에서는 behavior policy와 target policy를 동시에 improve 할 수 있다. Q-learning에서는 behavior policy μ는 ε-greedy로 target policy π는 greedy하게 선택하도록 한다. 각각 수렴 속도가 느리고, local optima에 빠질 수 있다는 단점을 해결하기 위해 적용된 절충안이다.
따라서 이제 다음과 같이 Q-learning이 진행된다.
-
현재 state S에서 behavior policy μ( ε-greedy)에 따라 action A를 선택한다.
-
q-function을 이용해서 다음 state S'에서의 action A'은 π(greedy)에 따라 선택한다.

-
Q-learning의 target은 다음과 같이 구한다.
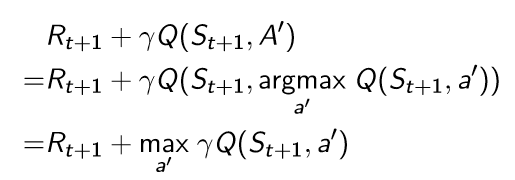
-
다음과 같이 최종 update를 수행한다.
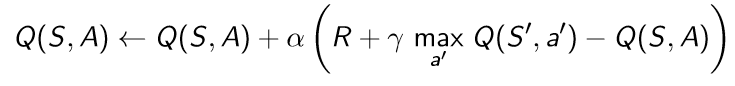
'Book > Reinforcement Learning' 카테고리의 다른 글
| [RL] Lecture 6. Value Function Approximation (0) | 2020.03.11 |
|---|---|
| [RL]Lecture 4. Model-Free Prediction (0) | 2020.02.05 |
| [RL]Lecture 3. Planning by Dynamic Programming (1) | 2020.01.29 |
| [RL]Lecture 2. Markov Decision Processes (0) | 2020.01.22 |
| [RL] Lecture 1. Introduction to Reinforcement Learning (0) | 2020.01.15 |