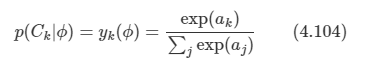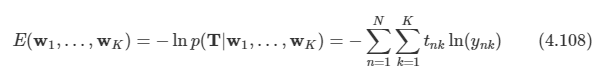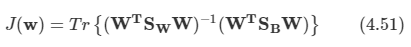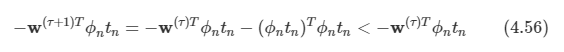케빈 머피의 Machine Learning 책을 보고 정리한 내용들입니다.

1.1 Machine Learning: what and why?

현재 우리는 빅데이터 시대에 살고 있으며, 수많은 양의 정보들을 마주하고 있다. 이러한 데이터들을 분석하기 위해 자동화된 데이터 분석 기법이 필요하게 되었고, 머신 러닝이 이러한 역할을 수행할 수 있다. 머신 러닝은 데이터의 패턴을 자동으로 인지하고, 다뤄지지 않은 패턴을 사용해 미래의 데이터를 예상하거나 불확실성 아래서 여러 종류의 결정을 선택하는 방법이다.

1.1.1 Types of machine learning

머신 러닝은 보통 두 개의 타입으로 구분할 수 있다.

1. Predictive, supervised learning
   • 레이블이 있는 입출력의 쌍이 주어졌을 때, 입력 x로 출력 y를 매핑하는 함수를 학습하는 것이 목표
   • 입력 x는 D차원 벡터로서 특징(feature), 속성(attribute), 공변량(covariance)라고 한다.
   • 출력 y는 한정된 값을 가지는 범주형 변수, 실수 값을 가지는 스칼라 변수가 있을 수 있다.
     • y가 범주형인 경우 분류(classification), 실수인 경우는 회귀(regression)이라고 한다.
2. Descriptive, unsupervised learning
   • 해당 방법에서는 입력만이 주어지고, 데이터 내의 흥미있는 패턴(interesting pattern)을 찾는 것이다.
   • 찾고자 하는 패턴이 주어지지 않기 때문에, 정의가 불분명하고, 에러를 측정할 수 있는 명확한 방법이 없다.
3. Reinforcement learning
   • 보상(reward)이 주어질 때 동작이나 행동을 배울 때 유용하다.
   • RL에 대해서는 이 책에서 자세히 다루지 않도록 한다.

1.2 Supervised learning

1.2.1 Classification

Classification의 목적은 입력 x로부터 출력 y를 매핑하는 것을 학습하는 것으로, y는 1~C의 값을 가지며, C는 class의 갯수를 의미한다. C=2인 경우에는 binary classification이라 하고, C > 2는 multiclass classification이라고 한다.
훈련 데이터에 대해서 학습을 하고 예측을 하는 것을 쉽기 때문에 classification의 주요 목적은 전에 보지 못했던 데이터들에 대해서도 답을 정확하게 예측하는 것(Generalization)이다.

1.2.1.2 The need for probabilistic predictions
주어진 입력 벡터 x와 훈련 집합 D에 대해 가능한 레이블들의 확률 분포를 나타낸다. 일반적으로 이 것은 길이가 C로 나타난다. 훈련 집합 D 뿐만 아니라 테스트 입력 x에 대한 조건부 확률이라는 것을 명시적으로 나타내기 위해 표기법에서 조건식 기호 | 의 오른쪽에 D와 x를 둔다.

확률적인 결과가 주어진다면, 다음의 식을 사용하여 레이블 값이 참인 경우에 대해 최선의 추측을 계산할 수 있다.

이 값은 가장 확률이 높은 클래스 레이블이고, 최대 사후 확률(MAP estimate) 로 알려져 있다. 해당 내용은 5.7에서 수학적인 검증을 한다.
다음과 같은 분야에서 실제로 응용되고 있다.

1. 문서 분류와 이메일 스팸 필터링
2. 꽃 분류
3. 이미지 분류와 글씨 인식
4. 얼굴 검출과 인식

1.2.2 Regression

Regression은 결과 변수가 연속적이라는 것을 제외하고 분류와 같다. 다음 그림은 단순한 예시를 보여준다.

다음은 실생활에 존재하는 Regression 문제의 예다.

• 현재 시장 상황과 다른 가능한 정보를 통해 다음 날의 주식 시장을 예측하는 것
• YouTube를 보는 사용자의 나이 예측
• 날씨 데이터와 시간, 문의 센서를 통해 건물 안의 온도를 예측하는 것

1.3 Unsupervised learning

Supervised learning과는 다르게 각 입력에 대해 기대되는 출력이 주어지지 않는다. 대신 작업을 확률 밀도 추정의 하나로 공식화한다. 즉, p(x|theta) 형태의 모형을 설계하는 것이 목표다. 이 말은 Unsupervised learning은 비조건적인 밀도 추정 문제에 해당한다.

1.3.1 Discovering clusters

Unsupervised learning의 기본이 되는 예제로 데이터를 그룹으로 clustering하는 문제다. 아래 그림은 210명의 키와 몸무게 대한 데이터들이다. 여러 개의 클러스터나 하위 그룹이 있는 것으로 보인다. K가 클러스터의 숫자를 의미한다고 하면, 첫 번째 목표는 p(K|D)를 예측하는 것이다. Supervised learning에서는 남자/여자와 같은 클래스가 있지만 Unsupervised learning은 클러스터의 갯수를 자유롭게 설정할 수 있다.
두 번째 목표는 각 데이터가 어떤 클러스터에 속하는지를 추정하는 것이다.(b)는 K=2일 때의 결과에 해당한다.

이 책에서는 model based clustering에 초점을 맞춘다. 모형 기반 클러스터링은 객관적인 방법으로 여러 모형을 비교할 수 있고, 여러 모형을 더 큰 시스템으로 조합할 수 있다.

클러스터링의 실제 응용은 다음과 같다.

• 천문학에서 천제 물리학의 측정값을 클러스터링하여 새로운 타입의 별을 발견할 수 있다.
• e-커머스에서 구입 내역과 웹 서핑을 분석하여 사용자들을 분석할 수 있고, 각 그룹에 타켓팅한 광고를 설정할 수 있다.

1.3.2 Discovering latent factors

고차원의 데이터를 처리할 때에는 데이터의 'essence'을 가지고 있는 작은 차원의 부분 공간으로 사영시키는 것이 유용하다.이것을 차원 축소라고 부른다. 아래 그림은 간단한 예시로, 3차원의 데이터를 2차원 평면으로 투영한 것이다.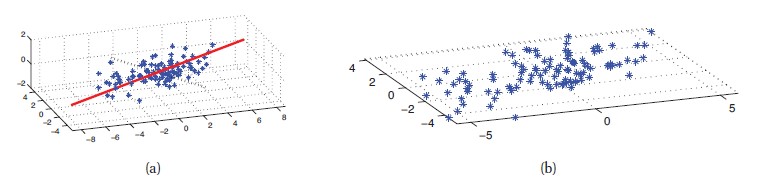

2차원 데이터로 투영한 (b)는 유사한 위치에 놓여 있는 것을 보아 결과가 좋게 나왔지만, 1차원으로 축소한 (a)의 빨간 선은 결과가 좋지 못하다. (해당 내용은 12장에서 더 자세히 다룬다.)
낮은 차원의 표현은 다른 통계 모형의 입력으로 사용하면 좀 더 예측 정확도가 높아진다. 이는 불필요한 특징을 거르기 때문이다. 차원 축소를 위한 가장 일반적인 접근은 주성분분석(Principal Componenet Analysis, PCA) 이다. 이는 linear regression의 비지도 버전과 같다. 고차원 응답 y를 관찰하지만, 저차원의 '원인' z는 발견하지 못한다. 이 모델은 z -> y 형태를 가지고 , 화살표를 뒤집어서 관찰된 고차원 y를 통해 잠재된 차원 z를 추정해야 한다.

1.3.3 Discovering graph structure

상관관계가 있는 변수를 측정하고, 가장 관련이 있는 것을 발견하려는 때가 있다. 이러한 구조는 그래프로 표현할 수 있다. 노드는 변수를 표현하고, 엣지는 변수 사이의 의존 관계를 표현한다.

1.3.4 Matrix completion

데이터가 손실되는 경우가 있다. 즉, 변수의 값을 모르는 경우가 발생할 수 있다. 따라서 이렇게 손실된 데이터에 타당한 값을 추정하는 것이며, 이것을 매트릭스 완성이라고 한다.

아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.

4.2 확률적 생성 모델

• 앞서 설명했던 용어들을 다시 한 번 정리하고 넘어간다.

  • 사후 확률 (posterior) : p(C_k|x)

    • 임의의 데이터 x가 주어졌을 때 이 데이터가 특정 클래스에 속할 확률

  • 클래스-조건부 밀도(class-conditional density) : p(x|C_k)

    • 특정 클래스에서 입력된 하나의 데이터 x가 발현될 확률

  • 가능도 함수 p(X|C_k)

    • 주어진 샘플 데이터가 실제 발현될 확률값을 주로 사용하며, 로그를 불이는게 일반적이다.

• 생성적 접근법을 사용해서 클래스가 2 개인 경우를 고려해본다. 그러면 C₁에 대한 사후 확률을 다음과 같이 적을 수 있다.

  

• σ(a)는 로지스틱 시그모이드 함수로서 다음과 같이 정의된다.

  

• 시그모이드 함수는 다음과 같이 그려진다.

  

• 시그모이드 함수는 다음과 같은 대칭성을 만족한다.

  

• 시그모이드는 0과 1 사이의 값으로 수렴을 하므로, 확률 값으로 고려를 해도 되고, 모든 점에서 연속이기 때문에 미분 가능해 수학적 전개에도 매우 편리하다.

• 로지스틱 시그모이드의 역(inverse)은 다음과 같다.

  

• 이를 로짓이라고 부른다.

---

• K > 2인 경우에도 식을 확장할 수 있다.

  • 이를 일반 선형 모델이라고 부른다.

    

  • a_k는 다음과 같다

    

  • 이를 정규화된 지수 함수라 하며, 다중 클래스 분류에 사용되는 식이 된다. 이를 softmax function이라고도 한다.

    • 평활화된 버전의 최댓값 함수에 해당한다.

4.2.1 연속적인 입력값(Continuous inputs)

• 클래스별 조건부 밀도가 가우시안이라고 가정하자.

  • 모든 클래스들이 같은 공분산 행렬을 공유한다고 가정하자.

  

• 이를 class가 2 개인 경우에 대해 고려해보자.

  

• 위 식은 σ(a)에 정의되어 있었다.

  

• 위와 같은 내용을 얻을 수 있다.

• x에 대한 2차 term이 모두 사라지면서 직선 식을 얻게 되었다.

  • 공분산 행렬을 공유한다는 가정으로 인해

• 같은 분산을 가지는 두 개의 가우시안 분포가 만나는 지점은 당연히 직선의 형태일 것이다.

  

• 왼쪽 그림은 2-class에서의 확률 밀도를 표현한 것이다.

  • 공분산이 동일하므로 모양이 같고, 따라서 경계면은 직선일 것이다.

• 이제 이를 K 클래스 문제로 확장하면 어떻게 될까?

  

• 계산을 간단히 하기 위해 공분산이 동일하다고 가정했지만 다르면 어떻게 될까?

  • 경계면을 구하는 식에서 이차항이 남게 되어 경계면이 곡선이 될 수 있다.

4.2.2 최대 가능도 해

• 클래스 조건부 밀도의 매개변수적 함수 형태를 명시하고 나면 최대 가능도 방법을 이용해서 매개변수들의 값과 사전 클래스 확률을 구할 수 있다.

  • 이를 위해 관측값 x와 그에 대한 데이터 집합이 필요하다.

• 두 개의 클래스가 있는 경우를 고려해보자.

  • 각각의 클래스들은 가우시안 클래스 조건부 밀도를 가지며, 공분산 행렬은 공유한다.

• t_n=1인 경우 C₁로, t_n=0인 경우 C₂로 분류한다.

• 따라서 가능도 함수는 다음과 같다.

  

• π 구하기

  • 로그 가능도 함수를 π에 대해 미분하여 관련된 항목만 모으면 된다.

    

• 여기서 N₁은 C₁에 속하는 샘플의 수이고, N₂은 C₂에 속하는 샘플의 수이다.

• π는 정확히 C₁에 속하는 샘플의 비율을 의미하게 된다.

• μ 구하기

  • 마찬가지로 로그 가능도 함수를 각각의 μ 값으로 미분하여 값을 구한다.

    

• 이 식을 0으로 놓고 μ₁, μ₂에 대해 풀면 다음을 얻을 수 있다.

  

• Σ 구하기

  • 역시 로그 가능도 함수를 미분하여 값을 구한다.

    

• 여기서 S는 다음과 같다.

  

4.2.3 이산 특징

• 입력 값이 연속적이지 않고 Discrete이라고 가정한다.

• 입력 데이터가 D차원이라면 각 class별로 얻을 수 있는 확률 분포의 실제 x의 Discrete 범위는 2^D개이다.

  • 이 중 독립 변수는 2^D-1이다. (합산 제약 조건 때문)

• 나이브 베이즈 가정을 사용했고 각 class C_k에 대해 조건부일 때 독립적으로 취급한다. 따라서 다음과 같다.

  

• 이 식을 4.63에 대입한다.

  

• 이는 다시 입력 변수 x_i에 대해 선형 함수다.

• 2-class에서는 시그모이드를 도입하면 동일할 것이다.

4.2.4 지수족

• 지금까지 사후확률의 경우 항상 sigmoid, softmax를 이용해서 모델링을 할 수 있었다.

  • 이를 더 일반화 시켜보자.

• 클래스 조건부 밀도가 지수족 분포를 따른다면 가능하다.

  • 지수족 분포를 따를 경우의 확률 분포는 다음의 형태로 적을 수 있다.

    

• 이 중 u(x) =x인 부분 집합들만 고려한다. 여기에 척도 매개변수 s를 도입해서 제한된 형태의 지수족 분포 클래스 조건부 밀도를 구할 수 있다.

• 각각의 클래스들의 각자의 매개변수 벡터를 가지지만, 척도 매개변수 s는 공유한다고 가정한다.

• 2-class에서 사용한 a_k에 대입하여 전개해본다.

  

• K-class에도 비슷하게 나오며 모두 선형 식임을 알 수 있다.

4.3 확률적 판별 모델

• 2-class 문제에 대해서는 사후 확률을 시그모이드 함수로 표현하고, k-class 문제에 대해서는 softmax 함수로 제동되는 것을 확인하였다.

• 다른 방식을 생각해본다

  • 선형 모델의 함수 형태를 명시적으로 사용하고, 최대 가능도 방법을 적용해 직접 구한다.

  • 이를 위해 iterative reweighted least squares, IRLS라고 한다.

• 앞에서 설명했던 간접적으로 매개변수를 찾는 방식은 생성적 모델의 예시이다.

• 이번 절에서는 판별적 훈련의 예시를 살펴볼 것이며, 적응 매개변수의 숫자가 더 적으며, 더 나은 예측 성능을 보일 수도 있다.

4.3.1 고정된 기저 함수

• 지금까지는 원 입력 벡터 x에 대해 직접적으로 적용되는 분류 모델에 대해 고려했다.

• 이제는 비선형 기저 함수를 이용하여 입력 값을 변환하는 형태를 사용한다.

  

• 위의 그림은 비선형 기저 함수를 이용하여 변환된 데이터를 선형 판별하는 것을 묘사하고 있다.

  • 왼쪽 그림은 최초 입력에 대한 공간을 나타내며 2개의 클래스로 구성되어 있음을 알 수 있다.

  • 오른쪽은 입력 데이터가 변환된 뒤, 선형 판별식에 의해 클래스가 구별되고 있음을 보여준다.

  • 왼쪽에서의 검은 원은 오른쪽에서는 선형으로 바뀐 것을 알 수 있다.

• ϕ₀(x)=1를 추가해서 w₀가 bias 역할을 수행하도록 한다.

• 실제의 여러 문제들에서는 클래스 조건 밀도들 사이에 상당한 중첩이 있다.

  • 각각의 값이 0과 1이 아닌 경우가 발생한다.

  • 하지만 ϕ(x)는 이러한 중첩 현상을 제거해주진 못한다.

    • 그렇지만 적절한 비선형성을 선택한다면 사후 확률을 모델링하는 과정이 쉬워지게 된다.

4.3.2 로지스틱 회귀

• 2-class에서 일반화된 선형 모델에 대해 알아보도록 하자. 분류에 대한 사후 확률 값은 로지스틱 회귀로 기술되는 것을 확인했다. 식은 다음과 같다.

  

• 여기서 σ 는 로지스틱 시그모이드라고 부른다.

• 기저 함수 ϕ 가 M차원이면 M개의 조절 가능한 매개변수를 가게 된다.

  • 최대 가능도 방법을 이용하여 가우시안 클래스 조건부 밀도를 근사했다면 평균값에 대해서는 2M개, 공분산 행렬에 대해서는 M(M+1)/2개의 매개변수를 가지게 되었을 것이다.

  • 사전 분포까지 고려한다면 M(M+5)/2+1 개의 파라미터가 필요하게 된다.

  • 따라서 M이 클 경우 로지스틱 회귀 모델을 직접 다루는 것이 더 유리할 수 있다.

• 최대 가능도 방법을 통해서 로지스틱 회귀 모델의 매개변수를 구할 수 있다.

  • 이를 위해서는 로지스틱 시그모이드의 미분값을 구해야 하고, 자세한 증명은 생략하도록 한다.

    

• 가능도 함수를 다음과 같이 적어보자.

  

  • n=1,2,...,N에 대해 t_n={0,1}이고, ϕ_n=ϕ(x_n)이다.

  • 가능도 함수의 음의 로그값을 취하여 오류 함수를 정의한다.

    

  • 이러한 형태를 cross entropy error function이라고 한다.

• 이를 w에 대하여 오류 함수의 기울기를 계산하면 다음과 같다.

  

  • 로그 가능도 함수의 기울기를 위한 간단한 형태의 식이 된다.

• 원한다면 한 번에 하나씩 데이터를 추가하여 순차적인 알고리즘을 만들 수 있다.

• 선형적으로 분리 가능한 데이터 집합에 대해 최대 가능도 방법을 사용하면 심각한 과적합 문제를 겪을 수 있다.

4.3.3. IRLS(Iterative reweighted least squares)

• 가우시안 노이즈 모델을 선정하여 식을 모델링했고, 이 식은 닫힌 형태이므로 최적의 해를 구할 수 있다.

  • w에 대해 이차 종속성을 가지고 있었기 때문

• 하지만 로지스틱 회귀 모델의 경우에는 sigmoid 함수의 비선형성으로 인해 해가 닫힌 형태가 아니다.

  • convex 형태이므로 유일한 최솟값을 가지고 있다.

  • Newton-Raphson 방식으로 쉽게 최소화가 가능하다.

    

• 선형 회귀 모델과 제곱합 오류 함수에 대해 Newton-Raphson 방법을 적용해본다.

  

• 여기에 그래디언트와 헤시안을 적용하도록 한다.

  

• Newton-Raphson 업데이트 식은 다음과 같다.

  

• 이 결과값은 표준 최소 제곱 해에 해당하고, 오류 함수는 이차식이며, 한 단계만에 정확한 해를 구할 수 있다.

---

• 이제 이 업데이트를 cross-entropy 오차함수에 적용해 본다.

  

• 여기서 R은 N x N인 대각 행렬이다.

• 헤시안이 더 이상 상수가 아니며, 가중 행렬 R을 통해서 w에 종속성을 가지고 있음을 알 수 있다.

• y_n이 0과 1 사이의 수 라는 사실로 부터 H의 속성을 이해할 수 있다.

  • 임의의 벡터 u에 대해 u^THu > 0 을 만족한다.

  • 헤시안 행렬은 양의 정부호 행렬이고, w에 대한 볼록 함수이다.

• 로지스틱 회귀 모델에 대한 Newton-Raphson 업데이트는 다음과 같다.

  

  • 여기서 z는 다음을 원소로 가지는 N차원 벡터다.

    

• R이 상수가 아니고, 파라미터 w에 영향을 받는 요소이므로 이를 반복 업데이트 방식으로 풀어야 한다.

  • 따라서 IRLS라고 부른다.

• 이렇게 가중치가 부여된 최소 제곱 문제는 가중치 대각 행렬 R을 분산으로 생각할 수 있다. 로지스틱 회귀 모델에서 t의 평균과 분산은 다음과 같기 때문이다.

  

• IRLS는 변수 a = w^T ϕ에 대해 선형 문제를 가진다.

  

4.3.4 다중 클래스 로지스틱 회귀

• 다중 클래스 분류 문제를 다루는 생성적 모델에서는 선형 함수인 softmax가 사용한다고 이야기했다.

  

• 클래스 조건부 분포와 사전 분포를 따로 구하기 위해 MLE나 베이지안 정리를 사용해서 사후 확률을 찾았다.

  • 이를 바탕으로 간접적으로 매개변수 w_k를 구했던 것이다.

  • w_k를 직접 구하기 위해 y_k에 대한 미분값이 필요하다.

    

  • 여기서 I_kj는 단위 행렬이다.

• 가능도 함수에 대해 알아 본다. one hot encoding을 사용해서 표현하도록 한다.

  

  • 여기서 y_nk=y_k( ϕ_n)이고, T는 N x K인 행렬이다.

  • 음의 로그값을 취하면 다음과 같이 된다.

    

  • 이를 cross-entropy라고 부른다.

• 매개변수 벡터 w_j에 대해서 오류 함수의 기울기를 취해 본다.

  

• 선형 모델에 제곱합 오류 함수를 사용하였을 경우와 로지스틱 회귀 모델에 교차 엔트로피 오류 함수를 사용하였을 경우에 기울기 함수의 형태가 같다는 것을 확인할 수 있다.

4.3.5 프로빗 회귀

• 지금까지 클래스 조건 분포가 지수족으로 표현 가능하며 사후 분포를 로지스틱 함수로서 표현할 수 있다는 것을 보았다.

• 그러나 단순한 형태의 사후 확률이 모든 종류의 클래스 조건부 밀도 분포에 대해 결과로 나오는 것은 아니다.

  • 가우시안 혼합 분포를 이용하면 불가능하다.

• 다른 종류의 판별적 확률 모델을 살펴보도록 한다.

  • 2개의 분류 문제를 가진 일반화된 선형 모델의 틀을 유지한다.

    

  • 여기서 a=w^T ϕ 이고, 함수 f는 활성 함수(activation function)가 된다.

• 노이즈 임계값 모델을 고려해서 연결 함수를 선택할 수 있다.

  • ϕ_n을 a_n=w^Tϕ_n으로 계산한 후, 다음에 따라 표적값을 설정한다.

    

  • 여기서 θ 는 확률 밀도 p( θ )에서 추출된다면 활성 함수는 다음과 같이 기술할 수 있다.

    

    

• 여기서 파란색 곡선은 p( θ )로 두 개의 가우시안 함수의 혼합으로 이루어진다.

• 이에 해당하는 누적 분포 함수 f(a)는 붉은색 곡선으로 그려져 있다.

• 파란색 곡선 상의 녹색 수직선에서의 값은 같은 지점에서의 붉은색 곡선의 기울기와 같다.

• 이제 p( θ )를 표준 정규 분포로 생각한다면 식을 다음과 같이 기술할 수 있다.

  

• 이 함수를 역프로빗 함수라고 부른다.

  • 시그모이드 함수의 모양과 비슷하게 생겼으므로 일반적인 가우시안 분포를 사용해도 이 모델은 그대로 유지된다.

  • 오차 함수는 다음과 같이 정의된다.

    

  • 이 함수는 보통 erf 함수 또는 에러 함수라고 부른다.

    • 머신 러닝 모델에서 사용중인 오류 함수와는 다른 것이다.

• 이 오차 함수는 역프로빗 함수와 다음과 같은 관계를 가진다.

  

• 역프로빗 활성화 함수를 바탕으로 한 일반화된 선형 모델을 프로빗 회귀라 한다.

---

• MLE 방법을 이용하여 프로빗 회귀의 매개변수를 구할 수 있다.

  • 로지스틱 회귀와 비슷한 경우가 많다.

• 실제 응용 사례에서 문제가 될 수 있는 것은 outlier이다.

  • 입력 벡터 x를 측정할 때, 오류가 발생하거나 표적 벡터 t를 잘못 라벨링했을 때, 이상값 문제가 발생한다.

  • 이러한 데이터는 분류기를 심각하게 왜곡할 수 있다.

  • 로지스틱 회귀 모델과 프로빗 회귀 모델은 서로 다른 반응을 보인다.

    • 로지스틱 모델은 x가 문한대로 감에 따라서 exp(-x)와 같이 감쇠되는 반면, 프로빗은 exp(-x²)와 같이 감쇠되므로 더 예민하게 반응한다.

• 하지만 두 모델 모두 데이터는 모두 정확하게 라벨링되어 있다고 가정한다.

4.3.6 정준 연결 함수

• 가우시안 노이즈 분포를 사용한 선형 회귀 모델에서 에러 함수는 음의 로그 가능도 함수를 사용한다.

  

• 여기서 매개변수 벡터 w에 대해 미분하면 오륫값에 특징 벡터를 곱한 형태를 띠게 된다.

• 이 결과가 타깃 변수의 조건부 분포가 지수족에 포함되는 경우에 일반적으로 얻을 수 있는 결과이다.

  • 이 경우의 활성화 함수를 정준 연결 함수(canonical link function)라 한다.

• 입력 벡터 x에 대해 지수족 함수 분포를 가정했지만 여기서는 타겟 값 t에 대해 가정한다.

  

• 일반화된 선형 모델은 y가 입력의 선형 결합을 비선형 함수에 넣은 결과로 표현되는 모델이라 정의된다.

  

  • 여기서 f()가 활성 함수이며, f^-1()가 연결 함수다.

• η 의 함수로 표현되는 이 모델의 로그 가능도 함수를 고려해보자.

  

• 모든 관측값들이 동일한 척도 매개변수를 공유한다고 가정한다.

  • s는 n에 대해 독립적이다.

• 모델 매개변수 w에 대해 미분하면 다음과 같다.

  

• 여기서 a_n=w^T ϕ _n이고, y_n=f(a_n)이다.

  

• f( ψ (y))=y 이고, 따라서 f'( ψ ) ψ '(y)=1이다.

• 또한 a=f^-1(y) 이므로 a = ϕ 이고, 결국 f'(a) ψ '(y)=1이 된다.

  

아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.

4. 선형 분류 모델

• 지금까지는 회귀 문제에 대해서만 다루어 보았지만 이번엔 분류 문제에 대해서 다루어 보도록 한다.

• 분류는 입력 벡터 x를 받았을 때 대응되는 클래스에 속하도록 하는 작업이다.
  • 이 때 클래스는 K개로 C_k 로 표기한다.
  • 하나의 데이터는 하나의 클래스에만 속하며, 하나의 클래스는 다른 클래스를 포함하지 않는다.
  • 이렇게 나누어진 영역을 decision region이라고 부르며 나누는 경계면을 decision boundaries라고 부른다.

4.1 판별 함수

4.1.1 두 개의 클래스

• 선형 판별식의 가장 간단한 형태를 다음과 같다.

• 여기서 w는 가중치 벡터라 부르고, w₀은 bias라고 부른다. 회귀랑 동일하다.

• 보통 2개의 클래스를 분류하는 문제에서 y(x)>=0인 경우를 C1으로 분류하고, 아닌 경우를 C2로 분류한다.

  • 이 때 decision boundaries는 y(x)=0임을 알 수 있다.

• 이제 임의의 두 점 x_A, x_B가 이 경계면 위에 있다고 하자.

  • 이 때 y(x_A)=y(x_B)=0를 만족하고, w^T(x_A−x_B)=0다. 여기서 w는 결정 경계에 대해 수직임을 알 수 있다.

  • 결정 경계에서 식을 전개하면 다음의 식을 얻을 수 있다.

    

• 이제 D=2라고 할 때 그림을 살펴본다.

  

• 임의의 한 점 x에 대해 결정 경계면에 수직으로 내린 지점을 x_ㅗ라고 하자.

• 이 경우 다음과 같은 식이 성립한다.

  

• 3장에서와 비슷하게 x₀=1를 이용하자.

  

• 위와 같이 간단하게 적을 수 있다.

4.1.2 다중 클래스

• K > 2인 상황을 다중 클래스라고 부른다.

  • 이 문제를 2-class 문제를 여러 개 조합해서 해결할 수 있다.
  • K-1개의 2-class 분류기가 있으면 K개의 클래스를 분류 가능하다.

  

• 왼쪽 그림을 보면 3개의 클래스를 분류하기 위해 2개의 2-class 문제를 사용하였다. 하지만 녹색 영역과 같이 판정을 할 수 없는 부분이 생기게 된다.

• 또한 만약 K(K-1)/2 개의 분류기를 사용해서 분류를 한다면 오른쪽과 같다.

  • 이 경우에도 녹색 영역과 같은 애매한 부분이 생긴다.

• 이 문제를 해결하기 위해 다른 방법을 사용한다.

  

• j != k일 때, y_k(x)>y_j(x)를 만족하면 x를 클래스 C_k로 판별하자.

  • 그러면 두 클래스 간의 decision boundaries는 y_k(x)=y_j(x)에서 형성된다.

  • 이 때 식을 전개하면,

    

  • 2-class 문제에서 사용하던 것과 같다.

• 이러한 판별 함수의 결정 경계는 언제나 단일하게 연결되어 있으며 볼록 성질을 가진다.

  • 모두 하나의 선으로 연결되어 있고, 내부의 어느 각도 180도를 넘지 않는다는 것과 같다.

  • 이를 확인할 수 있다.

    

    • x_A,x_B는 같은 지역의 임의의 두 점이다. x는 두 점 사이에 위치한 임의의 한 점을 나타내고, λ 는 0과 1 사이의 값이다.

      

    • y_k(x_A)>y_j(x_A) 이고 y_k(x_B)>y_j(x_B)이므로 y_k(xˆ)>y_j(xˆ)가 된다. 즉 아래 그림과 같다.

      

4.1.3 분류를 위한 최소 제곱법

• 최소제곱법을 사용해서 분류 문제를 해결해보자.

  • 사실 그리 정확하진 않다.

• 판별식은 다음과 같이 정의하고 간단히 정리하는 것이 가능하다.

  

• n번째 행이 t_n^T인 행렬 T와 n번째 행이 x

  _n^T라 하면, 전체 샘플 데이터를 X

  로 정의할 수 있다.

• 최소제곱법을 다음과 같이 적는다.

  

  • Tr은 행렬의 trace를 의미하며, trace는 행렬의 대각성분 합을 의미한다.

  • W에 대해 미분하고 정리하면 다음과 같다.

    

  • X^† 는 pseudo-inverse 행렬이다.

• 모든 훈련 집합의 표적 벡터들이 식 4.18의 선형 제약 조건을 어떠한 a와 b 값에 대해서 만족한다면 x 값에 대한 모델 예측값이나 제약 조건 4.19를 만족한다.

  

  

• 원 핫 인코딩을 통해 얻은 예측값들은 어떤 x의 경우에든 y(x)의 원소들을 전부 합하면 1이 된다.

  • 하지만 (0,1) 범위 내 안이라는 조건은 없으므로 확률값이라고 할 수 없다.

• 문제는 최소 제곱법은 outlier에 대해 너무 민감한 성질을 보인다. 따라서 더 강건한 모델을 고를 필요가 있다.

  

  • 녹색선은 로지스틱 회귀 분석으로 얻은 경계선, 보라색 선은 최소 제곱법을 사용한 것이다.
  • 보라색선은 우측의 그림처럼 outlier가 존재할 때 잘 분류하지 못하는 것을 알 수 있다.

4.1.4 피셔의 선형 판별

• 2-class 문제로 접근을 한다.

• D차원의 입력 벡터 x를 일차원에 투영한다고 해보자. 식은 다음과 같다.

  

• 이 식은 임의의 한 벡터를 한 차원의 벡터 위의 한 점(스칼라 값)으로 변환해준다.

• y에 임계값을 추가해 클래스를 분류하도록 한다.

• 높은 차원을 낮은 차원으로 줄였기 때문에 정보 손실은 당연하다.

  • 그렇기 때문에 정보 손실을 적게 하도록 해야 한다.

• w에 투영되었을 경우에 클래스 간의 분리 정도를 측정할 수 있는 가장 쉬운 방법은 투영된 클래스의 평균들이 얼마나 분리되어 있는가를 보는 것이다.

  

• 각 클래스의 평균을 나타내는 벡터를 표기할 수 있다.

• 이 값을 가지고 두 클래스간의 거리가 최대화되도록 하는 식을 전개한다.

• 1차원의 벡터로 투영된 후의 값은 다음과 같다.

  

• w를 찾아야 하는데, w 값만 무한정 커지면 값이 커지므로 단위 벡터로 고정을 한다.

• 이 식에 라그랑주 승수법을 적용해서 최소값을 구하면 w는 (m₂-m₁)에 비례한다.

• 왼쪽이 지금까지 한 방법인데 상당히 중복되는 것을 볼 수 있다. 이는 클래스 분포가 심한 비대각 공분산을 가지고 있기에 생긴다.

• 피셔의 제안은 투영된 클래스 평균 사이의 분리 정도를 크게 하는 동시에 각 클래스 내의 분산을 작게 하는 함수를 최대화함으로써 클래스 간의 중복을 최소화하는 것이다.

• 따라서 분산도를 정의한다.

  

• 여기서 y_n=w^Tx_n이다. 이 식은 투영 후 점들의 분산도를 의미한다.

  

• 최종 피셔 판별식은 위와 같으며, 정리하면 다음과 같은 식을 얻게 된다.

  

  • S_B는 클래스 간 공분산 행렬을 의미하고, S_W는 클래스 내 공분산 행렬을 의미한다.

    

  • J(w)를 w에 미분하면 최종적으로 위와 같은 식을 얻게 된다.

4.1.5 최소 제곱법과의 관계

• 에러 함수를 정의해본다.

  

• E는 w₀와 w에 대해 각각 미분하고 그 값을 0으로 설정하면 다음의 식을 얻게 된다.

  

• t_n은 다음과 같다.

  

  • N₁,N₂은 각 클래스에 속한 샘플 수를 의미하고 N은 전체 샘플 수를 의미한다.
  • C₁ = N/N₁, C₂=N₂

• m은 전체 데이터 집합의 평균이다.

  

• 4.32식에 x_n을 곱하고 전개하면 다음과 같다.

  

• 최종적으로 다음과 같으면 피셔 판별식과 동일하다.

  

4.1.6 다중 클래스에 대한 피셔 판별식

• 이제 K의 값이 2보다 큰 경우 피셔 판별식을 적용해보자.

  • 단 K<D임을 가정하자.

• D차원을 더 낮은 차원으로 변환하는 식을 아래와 같이 기술한다.

  

• W의 컬럼 개수는 D'로 정의한다. 당연히 D'의 값은 D보다 작다.

• 클래스 내 공분산 행렬

  • 앞서 살펴본 S_W를 K개의 클래스 버젼으로 확장한다.

  • N_k는 클래스 C_k에 속한 샘플의 수 이다.

    

• 클래스 간 공분산 행렬

  • 클래스 사이의 분산이 아닌 전체 데이터에 대한 공분산 행렬을 정의한다.

  • N은 전체 샘플 합계 : N=sum to k N_k

  • m은 전체 평균

    

  • 이 때 클래스 간 분산과 클래스 내 분산으로 나눌 수 있다.

  • 즉, S_T로 부터 S_W를 제외한 나머지를 S _B라고 정의한다.

    

  • 이 공분산 행렬들은 x 공간상에서 정의되었다. 행렬들을 투영된 D'차원의 y 공간상에서 정의해보자.

    

  • 에러 함수 만들 때, 여러 가지 선택지가 있지만 Fukunaga의 방법을 선택한다.

    

  • 투영 행렬 W에 대한 명시적인 함수로 다음과 같이 다시 적는다.

    

    • 이 기준을 최대화 하는 것은 어렵지 않지만 노력이 필요해서 Fukunaga에 설명되어 있다고 한다.

4.1.7 퍼셉트론 알고리즘

• 2-class에 대해 간단하게 알아보자.

  

• 활성 함수로 가장 간단한 형태인 계단형 함수를 쓴다.

  

• 여기서 ϕ ₀(x) = 1 이다. 표적값은 0,1 이 아닌 +1, -1로 정의해서 사용한다.

• 퍼셉트론에서 매개변수 w를 구하기 위한 알고리즘도 오류 함수를 최소화하는 방식이다.

  • 오분류된 패턴의 총 숫자를 오류 함수로 고를 수 있지만 사용하지 않는다.

    • 학습 알고리즘이 복잡해진다.
    • 오류 함수가 w에 대해 조각별 상수 함수다. w에 대한 변화가 결정 경계를 데이터 포인트들 중 하나를 건너 이동하게 하는 곳에서 불연속성이 발생한다.
      • 따라서 이 경우에 함수의 기울기를 통해서 w를 변경시키는 방법을 사용할 수 없다.

  • 따라서 퍼셉트론 기준이라는 오류 함수를 사용한다.

    

• 클래스 C₁에 대해서는 w^T ϕ (x_n) > 0이 되고, C₂는 w^T ϕ (x_n) < 0 을 만족하는 w를 찾고자 한다.

• 에러를 최소화 하는 방향으로 식을 전개해야 하므로 기울기 방법으로 w를 만들 수 있다.

  

  • η : 파라미터 학습 비율
  • τ : 알고리즘 스텝 인덱스

  

• 퍼셉트론의 동작 방식을 잘 설명하고 있는 그림이다.

  • 녹색 점이 오분류된 점인데 그에 따라 빨간색 방향만큼 보정이 된다.
  • 보정을 하고 난 뒤 다시 오분류된 점을 찾아 보정을 하는 작업을 계속해서 거치면 결정 경계가 완성된다.

• 아래 식을 통해 업데이트를 진행하면 에러가 점점 줄어든다는 것을 알 수 있다.

  

• 퍼셉트론 수렴 법칙(Perceptron convergence theorem)

  • 정확한 해를 가지고 있기만 한다면 퍼셉트론 학습 알고리즘은 정확한 해를 유한한 단계 안에 확실히 구할 수 있다.
    • 훈련 집합이 선형적으로 분리가 가능해야 한다.
  • 하지만 수렴을 위해 필요한 단계의 수가 매우 많을 수 있다.
    • 분리가 불가능한 문제인지, 단순히 수렴하는 데 오랜 시간이 걸리는 문제인지 구별이 불가능

• 퍼셉트론은 출력 값이 확률 값이 아니다.

• 중요한 제약 중 하나는 고정된 기저 함수의 선형 결합을 기반으로 한다.