CodeDrive

케빈 머피의 Machine Learning 책을 보고 정리한 내용들입니다.

1.4 Some basic concepts in machine learning

이번 절에서는 머신 러닝에서의 주요 아이디어를 제공한다. 뒷 파트에서 더 자세히 다룰 예정이기 때문에 여기서는 간략하게만 다룬다.

1.4.1 Parametric vs non-parametric models

이 책에서는 지도 학습과 비지도 학습에 따라서 확률 모형을 다르게 구성한다. 이런 모형을 정의하는 많은 방법이 있지만, 가장 중요한 차이는 모형이 고정된 개수의 변수(Parametric)를 갖는지, 혹은 훈련 데이터의 양에 따라 개수가 증가하는지(non-parametric) 여부다. Parametric한 모형은 빠르게 사용할 수 있는 장점이 있지만 데이터분포에 대한 강한 가정(데이터 분포에 영향을 많이 받는다.)을 만들기는 어렵다. non-parametric하면 데이터 분포에 영향을 덜 받지만 계산적으로 다루기 어렵다.

1.4.2 A simple non-parametric classifier: K-nearest neighbors

non-parametric 분류기의 가장 간단한 예를 K nearest neighbor (KNN) 분류기다. 이것은 데이터 집하에서 테스트 입력 x에 가장 가까이 에 있는 K개의 포인트를 찾는 것이며, 각 클래스의 멤버가 얼마나 이 집합에 있는지 개수를 계산하고, 실험적 비율을 추정 값으로 반환한다.

1.4.3 The curse of dimensionality

KNN 분류기는 간단하며, 레이블된 훈련 데이터가 충분하게 있다면 잘 작동한다. 하지만 KNN 분류기의 주요 문제는 고차원의 입력에 대해서는 잘 작동하지 않는다는 점이다. 고차원에서 성능이 잘 나오지 않는다는 것은 curse of dimensionality(차원의 저주) 때문이다.

1.4.4 Parametric models for classification and regression

차원의 저주에 대항하는 주요 방법은 데이터 분포의 성질에 관한 가정을 만드는 것이다. 귀납적 편향성이라고 불리는 이 가정은 parametric한 모델로 구현하며, 고정된 개수의 매개변수를 가지는 통계 모형이다. 폭넓게 사용되는 두 가지의 예를 살펴본다.

1.4.5 Linear regrssion

회귀에서는 선형 회귀(Linear regression)이라고 알려져 있는 것을 주로 사용한다. 이 모형에서는 입력에 대한 식을 1차 함수로 나타낸다. 다음과 같이 식을 표현한다.

여기서 x항은 입력벡터, w는 가중치 벡터라고 하며, 이들을 scalar 곱 형태로 나타낸다. 입실론 값은 선형 예측과 실제 응답 사이의 에러를 의미한다.
이 에러는 가우시안 또는 정규 분포를 갖는 것으로 가정한다. 선형 회귀와 가우시안과의 관계를 더 명시적으로 만들기 위해 다음의 형태로 모형을 다시 작성할 수 있다.

1.4.6 Logistic regression

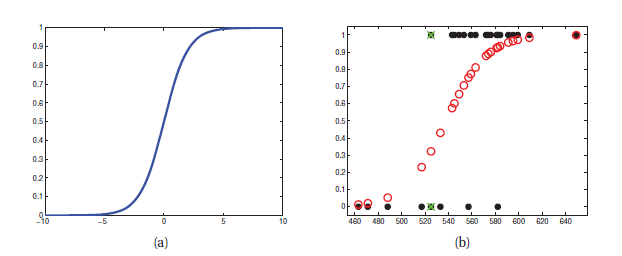
앞서 본 선형회귀를 두 가지만 변경한다면 일반화할 수 있다. 첫번째는 선형 회귀에서는 가우시안 분포라고 가정했던 것을 베르누이 분포라고 가정한다. y의 값이 0과 1만을 가진다면 다음과 같이 분포를 정의한다.

두 번째는 이전과 같이 식을 계산한 뒤에 0과 1 사이의 값을 가질 수 있도록 보장하는 함수인 sigmoid를 적용한다. sigmoid는 다음과 같이 적용한다.

sigmoid는 위와 같이 그래프가 그려지고, 값을 0과 1 사이의 수로 매핑하기 때문에 확률의 값을 나타낼 때 주로 사용한다. 두 변경을 모두 적용하면 다음과 같은 식을 얻을 수 있다.

이 식은 선형 회귀와 유사하기 때문에 로지스틱 회귀 분석이라고 부른다.

1.4.7 Overfitting

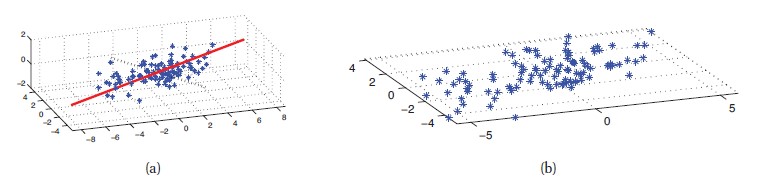
유연한 모델을 만들기 위해서 overfit(과적합)하지 않도록 주의해야 한다. 즉, 입력의 모든 변화를 모형화하는 것을 피해야 한다는 것으로, 이런 모형일 수록 노이즈인 경우가 많기 때문이다. 위와 같은 예시가 있을 수 있다. (b)가 모든 변화를 모형화를 한 경우에 해당된다. 하지만 실제 함수가 예시와 같이 생긴 확률을 낮기 때문에, 이런 모형을 사용해서 예측을 하는 경우 부정확한 결과를 얻을 수 있다.

1.4.8 Model selection

생략

1.4.9 No free lunch theorem

대부분의 머신 러닝의 알고리즘은 새로운 모델을 만들거나, 그것들이 적합하도록 만드는 것에 관심이 있다. 특정 문제에 대해서 최적화할 수 있지만, 모든 문제에 대해 최적의 모델은 없다. 이것을 No free lunch theorem 라고 한다. 하나의 영역에서 잘 작동하는 가정이 다른 영역에서 잘 작동하는 가정이 다른 영역에서 잘못 작동하는 경우가 있다.

케빈 머피의 Machine Learning 책을 보고 정리한 내용들입니다.

1.1 Machine Learning: what and why?

현재 우리는 빅데이터 시대에 살고 있으며, 수많은 양의 정보들을 마주하고 있다. 이러한 데이터들을 분석하기 위해 자동화된 데이터 분석 기법이 필요하게 되었고, 머신 러닝이 이러한 역할을 수행할 수 있다. 머신 러닝은 데이터의 패턴을 자동으로 인지하고, 다뤄지지 않은 패턴을 사용해 미래의 데이터를 예상하거나 불확실성 아래서 여러 종류의 결정을 선택하는 방법이다.

1.1.1 Types of machine learning

머신 러닝은 보통 두 개의 타입으로 구분할 수 있다.

1. Predictive, supervised learning
   • 레이블이 있는 입출력의 쌍이 주어졌을 때, 입력 x로 출력 y를 매핑하는 함수를 학습하는 것이 목표
   • 입력 x는 D차원 벡터로서 특징(feature), 속성(attribute), 공변량(covariance)라고 한다.
   • 출력 y는 한정된 값을 가지는 범주형 변수, 실수 값을 가지는 스칼라 변수가 있을 수 있다.
     • y가 범주형인 경우 분류(classification), 실수인 경우는 회귀(regression)이라고 한다.
2. Descriptive, unsupervised learning
   • 해당 방법에서는 입력만이 주어지고, 데이터 내의 흥미있는 패턴(interesting pattern)을 찾는 것이다.
   • 찾고자 하는 패턴이 주어지지 않기 때문에, 정의가 불분명하고, 에러를 측정할 수 있는 명확한 방법이 없다.
3. Reinforcement learning
   • 보상(reward)이 주어질 때 동작이나 행동을 배울 때 유용하다.
   • RL에 대해서는 이 책에서 자세히 다루지 않도록 한다.

1.2 Supervised learning

1.2.1 Classification

Classification의 목적은 입력 x로부터 출력 y를 매핑하는 것을 학습하는 것으로, y는 1~C의 값을 가지며, C는 class의 갯수를 의미한다. C=2인 경우에는 binary classification이라 하고, C > 2는 multiclass classification이라고 한다.
훈련 데이터에 대해서 학습을 하고 예측을 하는 것을 쉽기 때문에 classification의 주요 목적은 전에 보지 못했던 데이터들에 대해서도 답을 정확하게 예측하는 것(Generalization)이다.

1.2.1.2 The need for probabilistic predictions
주어진 입력 벡터 x와 훈련 집합 D에 대해 가능한 레이블들의 확률 분포를 나타낸다. 일반적으로 이 것은 길이가 C로 나타난다. 훈련 집합 D 뿐만 아니라 테스트 입력 x에 대한 조건부 확률이라는 것을 명시적으로 나타내기 위해 표기법에서 조건식 기호 | 의 오른쪽에 D와 x를 둔다.

확률적인 결과가 주어진다면, 다음의 식을 사용하여 레이블 값이 참인 경우에 대해 최선의 추측을 계산할 수 있다.

이 값은 가장 확률이 높은 클래스 레이블이고, 최대 사후 확률(MAP estimate) 로 알려져 있다. 해당 내용은 5.7에서 수학적인 검증을 한다.
다음과 같은 분야에서 실제로 응용되고 있다.

1. 문서 분류와 이메일 스팸 필터링
2. 꽃 분류
3. 이미지 분류와 글씨 인식
4. 얼굴 검출과 인식

1.2.2 Regression

Regression은 결과 변수가 연속적이라는 것을 제외하고 분류와 같다. 다음 그림은 단순한 예시를 보여준다.

다음은 실생활에 존재하는 Regression 문제의 예다.

• 현재 시장 상황과 다른 가능한 정보를 통해 다음 날의 주식 시장을 예측하는 것
• YouTube를 보는 사용자의 나이 예측
• 날씨 데이터와 시간, 문의 센서를 통해 건물 안의 온도를 예측하는 것

1.3 Unsupervised learning

Supervised learning과는 다르게 각 입력에 대해 기대되는 출력이 주어지지 않는다. 대신 작업을 확률 밀도 추정의 하나로 공식화한다. 즉, p(x|theta) 형태의 모형을 설계하는 것이 목표다. 이 말은 Unsupervised learning은 비조건적인 밀도 추정 문제에 해당한다.

1.3.1 Discovering clusters

Unsupervised learning의 기본이 되는 예제로 데이터를 그룹으로 clustering하는 문제다. 아래 그림은 210명의 키와 몸무게 대한 데이터들이다. 여러 개의 클러스터나 하위 그룹이 있는 것으로 보인다. K가 클러스터의 숫자를 의미한다고 하면, 첫 번째 목표는 p(K|D)를 예측하는 것이다. Supervised learning에서는 남자/여자와 같은 클래스가 있지만 Unsupervised learning은 클러스터의 갯수를 자유롭게 설정할 수 있다.
두 번째 목표는 각 데이터가 어떤 클러스터에 속하는지를 추정하는 것이다.(b)는 K=2일 때의 결과에 해당한다.

이 책에서는 model based clustering에 초점을 맞춘다. 모형 기반 클러스터링은 객관적인 방법으로 여러 모형을 비교할 수 있고, 여러 모형을 더 큰 시스템으로 조합할 수 있다.

클러스터링의 실제 응용은 다음과 같다.

• 천문학에서 천제 물리학의 측정값을 클러스터링하여 새로운 타입의 별을 발견할 수 있다.
• e-커머스에서 구입 내역과 웹 서핑을 분석하여 사용자들을 분석할 수 있고, 각 그룹에 타켓팅한 광고를 설정할 수 있다.

1.3.2 Discovering latent factors

고차원의 데이터를 처리할 때에는 데이터의 'essence'을 가지고 있는 작은 차원의 부분 공간으로 사영시키는 것이 유용하다.이것을 차원 축소라고 부른다. 아래 그림은 간단한 예시로, 3차원의 데이터를 2차원 평면으로 투영한 것이다.

2차원 데이터로 투영한 (b)는 유사한 위치에 놓여 있는 것을 보아 결과가 좋게 나왔지만, 1차원으로 축소한 (a)의 빨간 선은 결과가 좋지 못하다. (해당 내용은 12장에서 더 자세히 다룬다.)
낮은 차원의 표현은 다른 통계 모형의 입력으로 사용하면 좀 더 예측 정확도가 높아진다. 이는 불필요한 특징을 거르기 때문이다. 차원 축소를 위한 가장 일반적인 접근은 주성분분석(Principal Componenet Analysis, PCA) 이다. 이는 linear regression의 비지도 버전과 같다. 고차원 응답 y를 관찰하지만, 저차원의 '원인' z는 발견하지 못한다. 이 모델은 z -> y 형태를 가지고 , 화살표를 뒤집어서 관찰된 고차원 y를 통해 잠재된 차원 z를 추정해야 한다.

1.3.3 Discovering graph structure

상관관계가 있는 변수를 측정하고, 가장 관련이 있는 것을 발견하려는 때가 있다. 이러한 구조는 그래프로 표현할 수 있다. 노드는 변수를 표현하고, 엣지는 변수 사이의 의존 관계를 표현한다.

1.3.4 Matrix completion

데이터가 손실되는 경우가 있다. 즉, 변수의 값을 모르는 경우가 발생할 수 있다. 따라서 이렇게 손실된 데이터에 타당한 값을 추정하는 것이며, 이것을 매트릭스 완성이라고 한다.

아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.

1.4 차원의 저주

• 지금까지는 입력변수의 범위가 1차원 데이터였지만 현실에는 이러한 경우는 거의 없다.

• 이 데이터는 오일, 물, 가스가 혼합되어 운반되는 송유관에서 측정된 데이터다.

  • 이 데이터는 총 12 차원의 입력 벡터로 구성되어 있다.

  • 위 그림은 x6, x7의 차원을 표현한 산포도이다.

  • 점의 색깔은 데이터의 클래스를 의미한다.

  • x에 대해서 이 데이터가 어떤 클래스에 속할지를 판단해야 하는 문제이다.

• 가장 단순한 접근법은 입력 공간을 같은 크기의 여러 칸들로 나누는 것이다. x가 속한 셀 내에서 가장 많은 클래스를 확인한 뒤 그 클래스로 분류를 하는 방법이다.

  • 이 방법은 입력 변수가 더 많은 경우를 고려할 때 셀의 개수가 지수승만큼 증가하게 된다.

    

  • 판별 함수를 생각해보면 앞서 사용한 방식을 사용하면 구해야 할 차원 D^M까지 증가하게 된다.

    

---

• 고차원에서 발생할 수 있는 심각한 문제를 차원의 저주(curse of dimensionality)라고 부른다.

  • 저차원 공간에서 얻은 아이디어가 고차원 공간에서 반드시 적용되는지는 않다.

  • 고차원 입력값에 대해 사용할 수 있는 효과적인 패턴 인식 테크닉이 존재하긴 함.

    • 실제 세계의 고차원 데이터들의 경우에 유의미한 차원의 수는 제한적이다.

    • 실제 세계의 데이터는 보통 매끈한 특성을 가지고 있다.

1.5 결정 이론

• 결정 이론 : 불확실성이 존재하는 상황에서 의사 결정을 내려야 할 때 최적의 의사 결정을 내릴 수 있도록 하는 것

• 입력 벡터 x와 타깃 변수 벡터 t가 존재하는 상황에서 새로운 입력 벡터 x가 주어지면 타깃 변수 벡터 t를 예측하는 문제가 있다고 하자.

  • p(x,t)는 불확실성을 요약해서 나타내 줄 것이며 이 것을 찾아내는 것은 추론(inference) 문제의 대표적인 예시이다.

• 이런 확률 정보를 바탕으로 최적의 결정을 하려고 하는데 이를 결정 단계라고 한다.

  

1.5.1. 오분류 비율의 최소화

• 잘못된 분류 결과의 숫자를 가능한 줄이는 것이 목표이다. 이를 위해 x를 가능한 클래스들 중 하나에 포함시키는 규칙이 필요하다.

  • 이 규칙은 입력 공간을 결정 구역이라는 Rk들로 나누게 될 것이며 Rk에 존재하는 포인트들은 클래스 Ck에 포함될 것이다.

  • 이때 각 구역의 경계면을 결정 경계, 결정 표면이라고 부른다.

• 잘못 분류할 결과를 확률 식으로 표현할 수 있다.

  

  • 따라서 이를 최소화하는 방향으로 모델을 설계해야 한다.

1.5.2. 기대 손실 최소화

• 현실적으로 오분류의 수를 줄이는 것으로는 부족하다.

  • 따라서 암의 진단 예제의 경우에서 오분류를 하는 경우를 생각해보자.

    • case1 : 실제로 암이 아닌데 암이라고 진단할 경우

      • 환자의 기분은 나쁠 수 있지만 추가 검사를 통해서 아니라는 것을 밝혀낼 수 있다.

    • case2 : 실제로 암인데 암이 아니라고 진단할 경우

      • 이 경우에는 제 때에 치료를 받지 못하게 되어 죽음이라는 결과를 얻을 수 있다.

  • 즉 case1보다 case2가 심각한 경우이므로 case2에 더 강한 페널티를 부여하는 것이 필요하다.

• 이를 위해 cost function, loss function이라는 개념을 도입해서 이러한 문제들을 공식화할 수 있다.

  • 하나의 샘플 x가 실제로는 특정 클래스 Ck에 속하지만 이 샘플의 클래스를 Ci로 선택할 때 들어가는 비용이라고 정의한다.

  • 모든 경우에 대한 Loss를 정의한 것을 loss matrix라고 한다.

• Loss 함수를 최소화하는 해가 최적의 해인데 Loss 함수에 대한 평균값을 최소화하는 방법을 사용한다.

  

  • 각각의 x 값은 결정 구역 Rj들 중 하나에 독립적으로 포함된다. 그렇기 때문에 에러 값이 최소가 되는 Rj를 선택해야 한다.

  • 결국 x에 대해서

    

    를 최소화하는 클래스를 찾으면 된다.

  • 

    로 치환 가능하고, p(x)는 클래스마다 동일하다고 생각하고 생략한다.

  • 새로운 xnew가 들어왔을 때, 이 식을 사용한다.

1.5.3 거부 옵션

• 사후 확률 또는 결합 확률이 1에 가까운 것이 아니라 클래스 별로 비슷할 경우 분류에 대한 에러가 커지게 된다.

• 이러한 범위에 존재하는 x에 대해 특정한 클래스로 할당을 하는 것이 힘들기 때문에 결정을 회피하게 되는데 이를 reject option이라고 한다.

  

• 즉 그림을 보면 특정 수준(threshold)를 넘지 못하면 클래스 분류를 하지 않는 것이다.

  • 1/K<theta<1로 고려를 하며 theta를 조절해 거부되는 예시의 수를 조절할 수 있다.

1.5.4. 추론과 결정

• 지금까지 분류 문제를 두 개의 단계로 나누어서 알아보았다.

  • 추론 단계 : 훈련 집단을 활용하여 p(Ck|x)에 대한 모델을 학습시키는 단계

  • 결정 단계 : 학습된 사후 확률들을 이용해서 최적의 클래스 할당을 시행

• 결정 문제를 푸는 데에는 세 가지 다른 접근법이 있으며, 복잡도가 높은 순으로 설명한다.

• 생성 모델(generative model)

  • 각 클래스에 대해서 조건부 확률 밀도와 사전 확률을 따로 구해 사후 확률을 추론함.

    

  • 결합 분포를 모델링한 후 정규화를 통해 사후 확률을 구할 수 있음.

  • 이렇게 입력값과 출력값의 분포를 모델링하는 방식을 생성 모델이라고 하며, 이 분포로부터 새로운 샘플을 생성할 수 있는 능력이 있다.

• 판별 모델(discriminative model)

  • 사후 확률을 계산하는 추론 문제를 풀어낸 후에 결정 이론을 적용하여 각각의 입력 변수 x에 대한 클래스를 구한다. 사후 확률을 직접 모델링하는 이러한 방식을 판별 모델이라고 한다.

• 판별 함수(discriminative function)

  • 각각의 입력값을 클래스에 사상하는 판별 함수를 찾는다. 베이즈 확률 모델에 의존하지 않고 판별식을 찾아내는 방식이다.

---

• 세 가지 방식의 장단점에 대해서 논의해보자.

  • 생성 모델

    • 가장 복잡한 방식으로 x, Ck에 대해서 결합 분포를 찾아야 하는데 대부분의 사례에서 고차원이며 많은 훈련 집합을 필요로 한다.

    • 이 모델의 장점은 이 식을 이용해서 데이터의 주변 밀도도 구할 수 있다. 이를 바탕으로 발생 확률이 낮은 새 데이터(outlier)를 발견할 수 있다.

  • 판별 모델

    • 사후 확률을 계산하는 방식이 생성 모델보다 간편하다.

    • 클래스별 조건부 분포는 사후 확률에 많은 영향을 주지 않는다.

  • 판별 함수

    • 입력 공간을 결정 공간에 바로 매핑시키는 방식이다. 추론 단계와 결정 단계를 하나의 학습 문제로 합친 것이다.

    • 확률론을 다루지 않으므로 사후 확률을 알지 못하게 된다.

---

• 사후 확률을 구하는 것의 유의미한 이유는 다음과 같은 이유들 때문이다.

• 위험의 최소화

  • Loss matrix가 시간에 따라 바뀔 수도 있다.

  • 이는 사후 확률을 알고 있다면 쉽게 최소 위험 결정 기준을 구할 수 있다.

• 거부 옵션

  • 사후 확률을 알고 있으면 거부 기준을 쉽게 구할 수 있다.

• 클래스 사전 확률에 대한 보상

  • 클래스의 발현 비율이 다른 경우 이를 해결하기 위해 모델을 수정하게 된다.

  • 수정된 데이터 집합을 사용하여 사후 확률에 대한 모델을 찾아내고 이를 통해 사전 집합을 구할 수 있다.

• 모델들의 결합

  • 복잡한 문제를 좀 더 작은 문제로 나누어 해결하고 조합해서 사용된다.

  • 간단한 모델로 나누고 이를 독립적으로 가정하고 식을 나열한다.

  • 이를 조건부 독립이라고 하며 사후 분포에 대해서도 식을 전개할 수 있다.

  • 하나의 어려운 결합 확률을 구하는 대신에 모델링이 쉬운 두 개의 사후 확률을 구해 이를 결합하는 것이다.

    

1.5.5 회귀에서의 손실 함수

• 지금까지 분류에 대해서 알아보았으니 회귀에 대해서도 손실 함수를 알아본다.

  

• 회귀 함수의 손실 함수는 위와 같은 식이며 분류와 같이 기대 손실 함수로 사용한다. 보통 L(t, y(x))를 {y(x)-t}^2으로 사용한다.

  

• 그래서 위와 같은 식을 얻게 되고 우리의 목표는 E [L]을 최소화하는 y(x)를 찾는 것이다. 이는 미분을 통해서 구할 수 있다.

  

• 이는 x가 주어졌을 때의 t의 조건부 평균으로써 회귀 함수라고 한다. 다음 그림을 참고하면 이해가 더 쉬울 것이다.

  

• 다른 방식으로도 도출할 수 있는데 최적의 해가 조건부 기댓값이라는 지식을 바탕으로 식을 전개할 수 있다.

  

  • E [t|x]를 빼고 더한 것으로 아무런 영향을 주진 않는다. 수학적으로 정답인 평균값이다.

  • y(x) 샘플 데이터로부터 만들어진 모델 함수로 우리가 예측한 근사 식이다.

    

  • 전개식을 정리하면 위와 같아지게 된다. 크게 두 부분으로 나누어진다.

    • 첫 번째 term은 모델 y(x)와 관련된 요소로 조건부 평균을 통해 최소화하는 항이다.

    • 두 번째 term은 분산으로 샘플이 포함하고 있는 노이즈를 의미한다.

---

• 분류에서도 최적의 결정을 내리기 위한 방법들이 있었는데, 회귀에서도 다음과 같은 접근법들이 있다.

  • 결합 밀도를 구하는 추론하는 방법, 이 식을 정규화하여 조건부 밀도를 구하고 최종적으로 조건부 평균을 구한다.

  • 조건부 밀도를 구하는 추론 문제를 풀고 조건부 평균을 구한다.

  • 훈련 데이터로부터 회귀 함수 y(x)를 구한다.

1.6 정보이론

• 이산 확률 변수 x를 고려해 보자. 이 변수가 특정 값을 가지고 있는 것을 확인했을 때 전해지는 정보량은 얼마만큼일까?

  • 정보의 양은 '학습에 있어 필요한 놀람의 정도'로 해석하면 된다.

    • 따라서 항상 일어나는 일은 0이 될 것이다.

    • 그렇기 때문에 확률 분포 p(x)에 종속적이게 된다.

• 정보의 양을 h(x)라고 정의하면 정보는 결국 확률 함수의 조합으로 표현이 되게 될 것이다.

  

• 정보의 양을 나타내는 함수 h(x)는 확률 함수 p(x)의 음의 로그 값이다.

  • 음의 부호는 정보량이 음의 값을 가지지 않도록 하기 위해 붙여졌다.

  • 로그의 밑은 임의로 정하는데 보통 2를 선택하고 h(x)의 단위는 비트가 될 것이다.

• 이때 전송에 필요한 정보량의 평균치는 다음과 같이 구할 수 있다.

  

• 이 식은 매우 중요한데 이를 엔트로피(entropy)라고 정의한다.

  • 엔트로피는 평균 정보량을 의미하며, p(x)인 분포에서 h(x) 함수의 기댓값을 의미하게 된다.

• noiseless coding theorem

  • 엔트로피는 랜덤 변수의 상태를 전송하는데 필요한 비트 수의 하한선

• N개의 동일한 물체가 몇 개의 통 안에 담겨 있다고 가정해 보자.

  • i번째 통 안에 ni개의 물체가 담기도록 한다.

  • 전체 영역에 N개의 물체가 무작위로 놓여있다고 하고, 총 나타날 수 있는 가지 수는 N! 이 된다.

  • 하지만 물체들이 어떤 순서로 놓여 있는지는 중요하지 않다. 개수만이 중요할 뿐이다. 따라서 총 가지 수는 다음과 같다.

    

  • 이 것을 다중도(multiplicity)라고 부른다.

  • 로그를 붙이고 적당한 상수를 넣어 식을 정리하자.

    

  • 비율을 그대로 유진 상태에서 N->무한대를 취하고 **Stirling’s approximation** 을 적용하도록 한다.

    

  • 이 것을 적용하면

    

  • 통 안의 물체들의 순서를 미시 상태라 하며, ni/N으로 표현되는 통 각각이 가지고 있는 물체의 숫자 비율을 일컬어 거시 상태라 한다. 다중도 W를 거시 상태의 가중치라 일컫기도 한다.

  • N -> 무한대이고, ni/N이 고정된 상수라고 하면,

    

• 연속 변수일 때에는 식이 복잡하므로 생략하도록 한다.

1.6.1. 연관 엔트로피와 상호 정보

형태를 모르는 확률 분포 p(x)가 있다고 해보자. 그리고 이 확률 분포를 근사한 q(x)가 있다고 하자. 그러면 q(x)는 근사한 것이므로 정보량이 차이가 있다.

• p(x)가 아닌 q(x)를 사용했기 때문에 추가적으로 필요한 정보량의 기댓값을 정의한다.

  

• 위 정의를 Kullback-Leibler divergence, KL divergence

  • 근사 분포인 q(x)를 사용했기 때문에 정보량은 - ln q(x)을 사용한다.

  • 하지만 데이터는 p(x)이므로 기댓값은 실 분포를 대상으로 구하게 된다.

• 

  을 만족한다. (non-symmetric) 그리고 항상 0보다 큰 값을 가진다.

  • 만약 p(x),q(x) 이면 KL = 0이다.

• KL divergence는 다음과 같이 유도할 수 있다.

  

• 정보 이론은 중요하지만 복잡한 내용이 많으므로 위와 같이 간략히 소개하고 추후 더 자세히 소개하는 시간을 가지도록 한다.