아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
4.2 확률적 생성 모델
앞서 설명했던 용어들을 다시 한 번 정리하고 넘어간다.
사후 확률 (posterior) : p(Ck|x)
- 임의의 데이터 x가 주어졌을 때 이 데이터가 특정 클래스에 속할 확률
클래스-조건부 밀도(class-conditional density) : p(x|Ck)
- 특정 클래스에서 입력된 하나의 데이터 x가 발현될 확률
가능도 함수 p(X|Ck)
- 주어진 샘플 데이터가 실제 발현될 확률값을 주로 사용하며, 로그를 불이는게 일반적이다.
생성적 접근법을 사용해서 클래스가 2 개인 경우를 고려해본다. 그러면 C1에 대한 사후 확률을 다음과 같이 적을 수 있다.

σ(a)는 로지스틱 시그모이드 함수로서 다음과 같이 정의된다.
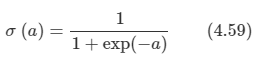
시그모이드 함수는 다음과 같이 그려진다.

시그모이드 함수는 다음과 같은 대칭성을 만족한다.

시그모이드는 0과 1 사이의 값으로 수렴을 하므로, 확률 값으로 고려를 해도 되고, 모든 점에서 연속이기 때문에 미분 가능해 수학적 전개에도 매우 편리하다.
로지스틱 시그모이드의 역(inverse)은 다음과 같다.

이를 로짓이라고 부른다.
K > 2인 경우에도 식을 확장할 수 있다.
이를 일반 선형 모델이라고 부른다.

ak는 다음과 같다

이를 정규화된 지수 함수라 하며, 다중 클래스 분류에 사용되는 식이 된다. 이를 softmax function이라고도 한다.
- 평활화된 버전의 최댓값 함수에 해당한다.
4.2.1 연속적인 입력값(Continuous inputs)
클래스별 조건부 밀도가 가우시안이라고 가정하자.
- 모든 클래스들이 같은 공분산 행렬을 공유한다고 가정하자.

이를 class가 2 개인 경우에 대해 고려해보자.

위 식은 σ(a)에 정의되어 있었다.

위와 같은 내용을 얻을 수 있다.
x에 대한 2차 term이 모두 사라지면서 직선 식을 얻게 되었다.
- 공분산 행렬을 공유한다는 가정으로 인해
같은 분산을 가지는 두 개의 가우시안 분포가 만나는 지점은 당연히 직선의 형태일 것이다.

왼쪽 그림은 2-class에서의 확률 밀도를 표현한 것이다.
- 공분산이 동일하므로 모양이 같고, 따라서 경계면은 직선일 것이다.
이제 이를 K 클래스 문제로 확장하면 어떻게 될까?

계산을 간단히 하기 위해 공분산이 동일하다고 가정했지만 다르면 어떻게 될까?
- 경계면을 구하는 식에서 이차항이 남게 되어 경계면이 곡선이 될 수 있다.
4.2.2 최대 가능도 해
클래스 조건부 밀도의 매개변수적 함수 형태를 명시하고 나면 최대 가능도 방법을 이용해서 매개변수들의 값과 사전 클래스 확률을 구할 수 있다.
- 이를 위해 관측값 x와 그에 대한 데이터 집합이 필요하다.
두 개의 클래스가 있는 경우를 고려해보자.
- 각각의 클래스들은 가우시안 클래스 조건부 밀도를 가지며, 공분산 행렬은 공유한다.

tn=1인 경우 C1로, tn=0인 경우 C2로 분류한다.
따라서 가능도 함수는 다음과 같다.

π 구하기
로그 가능도 함수를 π에 대해 미분하여 관련된 항목만 모으면 된다.

여기서 N1은 C1에 속하는 샘플의 수이고, N2은 C2에 속하는 샘플의 수이다.
π는 정확히 C1에 속하는 샘플의 비율을 의미하게 된다.
μ 구하기
마찬가지로 로그 가능도 함수를 각각의 μ 값으로 미분하여 값을 구한다.

이 식을 0으로 놓고 μ1, μ2에 대해 풀면 다음을 얻을 수 있다.

Σ 구하기
역시 로그 가능도 함수를 미분하여 값을 구한다.

여기서 S는 다음과 같다.

4.2.3 이산 특징
입력 값이 연속적이지 않고 Discrete이라고 가정한다.
입력 데이터가 D차원이라면 각 class별로 얻을 수 있는 확률 분포의 실제 x의 Discrete 범위는 2D개이다.
- 이 중 독립 변수는 2D-1이다. (합산 제약 조건 때문)
나이브 베이즈 가정을 사용했고 각 class Ck에 대해 조건부일 때 독립적으로 취급한다. 따라서 다음과 같다.
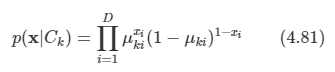
이 식을 4.63에 대입한다.

이는 다시 입력 변수 xi에 대해 선형 함수다.
2-class에서는 시그모이드를 도입하면 동일할 것이다.
4.2.4 지수족
지금까지 사후확률의 경우 항상 sigmoid, softmax를 이용해서 모델링을 할 수 있었다.
- 이를 더 일반화 시켜보자.
클래스 조건부 밀도가 지수족 분포를 따른다면 가능하다.
지수족 분포를 따를 경우의 확률 분포는 다음의 형태로 적을 수 있다.

이 중 u(x) =x인 부분 집합들만 고려한다. 여기에 척도 매개변수 s를 도입해서 제한된 형태의 지수족 분포 클래스 조건부 밀도를 구할 수 있다.

각각의 클래스들의 각자의 매개변수 벡터를 가지지만, 척도 매개변수 s는 공유한다고 가정한다.
2-class에서 사용한 ak에 대입하여 전개해본다.

K-class에도 비슷하게 나오며 모두 선형 식임을 알 수 있다.
4.3 확률적 판별 모델
2-class 문제에 대해서는 사후 확률을 시그모이드 함수로 표현하고, k-class 문제에 대해서는 softmax 함수로 제동되는 것을 확인하였다.
다른 방식을 생각해본다
선형 모델의 함수 형태를 명시적으로 사용하고, 최대 가능도 방법을 적용해 직접 구한다.
이를 위해 iterative reweighted least squares, IRLS라고 한다.
앞에서 설명했던 간접적으로 매개변수를 찾는 방식은 생성적 모델의 예시이다.
이번 절에서는 판별적 훈련의 예시를 살펴볼 것이며, 적응 매개변수의 숫자가 더 적으며, 더 나은 예측 성능을 보일 수도 있다.
4.3.1 고정된 기저 함수
지금까지는 원 입력 벡터 x에 대해 직접적으로 적용되는 분류 모델에 대해 고려했다.
이제는 비선형 기저 함수를 이용하여 입력 값을 변환하는 형태를 사용한다.

위의 그림은 비선형 기저 함수를 이용하여 변환된 데이터를 선형 판별하는 것을 묘사하고 있다.
왼쪽 그림은 최초 입력에 대한 공간을 나타내며 2개의 클래스로 구성되어 있음을 알 수 있다.
오른쪽은 입력 데이터가 변환된 뒤, 선형 판별식에 의해 클래스가 구별되고 있음을 보여준다.
왼쪽에서의 검은 원은 오른쪽에서는 선형으로 바뀐 것을 알 수 있다.
ϕ0(x)=1를 추가해서 w0가 bias 역할을 수행하도록 한다.
실제의 여러 문제들에서는 클래스 조건 밀도들 사이에 상당한 중첩이 있다.
각각의 값이 0과 1이 아닌 경우가 발생한다.
하지만 ϕ(x)는 이러한 중첩 현상을 제거해주진 못한다.
- 그렇지만 적절한 비선형성을 선택한다면 사후 확률을 모델링하는 과정이 쉬워지게 된다.
4.3.2 로지스틱 회귀
2-class에서 일반화된 선형 모델에 대해 알아보도록 하자. 분류에 대한 사후 확률 값은 로지스틱 회귀로 기술되는 것을 확인했다. 식은 다음과 같다.

여기서 σ 는 로지스틱 시그모이드라고 부른다.
기저 함수 ϕ 가 M차원이면 M개의 조절 가능한 매개변수를 가게 된다.
최대 가능도 방법을 이용하여 가우시안 클래스 조건부 밀도를 근사했다면 평균값에 대해서는 2M개, 공분산 행렬에 대해서는 M(M+1)/2개의 매개변수를 가지게 되었을 것이다.
사전 분포까지 고려한다면 M(M+5)/2+1 개의 파라미터가 필요하게 된다.
따라서 M이 클 경우 로지스틱 회귀 모델을 직접 다루는 것이 더 유리할 수 있다.
최대 가능도 방법을 통해서 로지스틱 회귀 모델의 매개변수를 구할 수 있다.
이를 위해서는 로지스틱 시그모이드의 미분값을 구해야 하고, 자세한 증명은 생략하도록 한다.
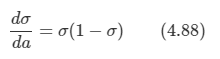
가능도 함수를 다음과 같이 적어보자.

n=1,2,...,N에 대해 tn={0,1}이고, ϕn=ϕ(xn)이다.
가능도 함수의 음의 로그값을 취하여 오류 함수를 정의한다.

이러한 형태를 cross entropy error function이라고 한다.
이를 w에 대하여 오류 함수의 기울기를 계산하면 다음과 같다.

- 로그 가능도 함수의 기울기를 위한 간단한 형태의 식이 된다.
원한다면 한 번에 하나씩 데이터를 추가하여 순차적인 알고리즘을 만들 수 있다.
선형적으로 분리 가능한 데이터 집합에 대해 최대 가능도 방법을 사용하면 심각한 과적합 문제를 겪을 수 있다.
4.3.3. IRLS(Iterative reweighted least squares)
가우시안 노이즈 모델을 선정하여 식을 모델링했고, 이 식은 닫힌 형태이므로 최적의 해를 구할 수 있다.
- w에 대해 이차 종속성을 가지고 있었기 때문
하지만 로지스틱 회귀 모델의 경우에는 sigmoid 함수의 비선형성으로 인해 해가 닫힌 형태가 아니다.
convex 형태이므로 유일한 최솟값을 가지고 있다.
Newton-Raphson 방식으로 쉽게 최소화가 가능하다.
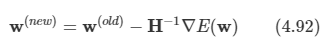
선형 회귀 모델과 제곱합 오류 함수에 대해 Newton-Raphson 방법을 적용해본다.

여기에 그래디언트와 헤시안을 적용하도록 한다.

Newton-Raphson 업데이트 식은 다음과 같다.

이 결과값은 표준 최소 제곱 해에 해당하고, 오류 함수는 이차식이며, 한 단계만에 정확한 해를 구할 수 있다.
이제 이 업데이트를 cross-entropy 오차함수에 적용해 본다.

여기서 R은 N x N인 대각 행렬이다.

헤시안이 더 이상 상수가 아니며, 가중 행렬 R을 통해서 w에 종속성을 가지고 있음을 알 수 있다.
yn이 0과 1 사이의 수 라는 사실로 부터 H의 속성을 이해할 수 있다.
임의의 벡터 u에 대해 uTHu > 0 을 만족한다.
헤시안 행렬은 양의 정부호 행렬이고, w에 대한 볼록 함수이다.
로지스틱 회귀 모델에 대한 Newton-Raphson 업데이트는 다음과 같다.
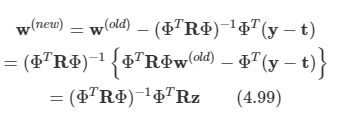
여기서 z는 다음을 원소로 가지는 N차원 벡터다.

R이 상수가 아니고, 파라미터 w에 영향을 받는 요소이므로 이를 반복 업데이트 방식으로 풀어야 한다.
- 따라서 IRLS라고 부른다.
이렇게 가중치가 부여된 최소 제곱 문제는 가중치 대각 행렬 R을 분산으로 생각할 수 있다. 로지스틱 회귀 모델에서 t의 평균과 분산은 다음과 같기 때문이다.

IRLS는 변수 a = wT ϕ에 대해 선형 문제를 가진다.
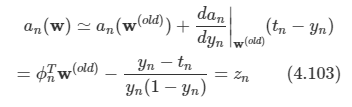
4.3.4 다중 클래스 로지스틱 회귀
다중 클래스 분류 문제를 다루는 생성적 모델에서는 선형 함수인 softmax가 사용한다고 이야기했다.

클래스 조건부 분포와 사전 분포를 따로 구하기 위해 MLE나 베이지안 정리를 사용해서 사후 확률을 찾았다.
이를 바탕으로 간접적으로 매개변수 wk를 구했던 것이다.
wk를 직접 구하기 위해 yk에 대한 미분값이 필요하다.

여기서 Ikj는 단위 행렬이다.
가능도 함수에 대해 알아 본다. one hot encoding을 사용해서 표현하도록 한다.

여기서 ynk=yk( ϕn)이고, T는 N x K인 행렬이다.
음의 로그값을 취하면 다음과 같이 된다.
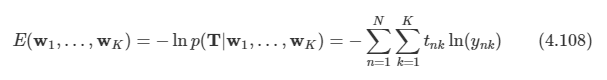
이를 cross-entropy라고 부른다.
매개변수 벡터 wj에 대해서 오류 함수의 기울기를 취해 본다.

선형 모델에 제곱합 오류 함수를 사용하였을 경우와 로지스틱 회귀 모델에 교차 엔트로피 오류 함수를 사용하였을 경우에 기울기 함수의 형태가 같다는 것을 확인할 수 있다.
4.3.5 프로빗 회귀
지금까지 클래스 조건 분포가 지수족으로 표현 가능하며 사후 분포를 로지스틱 함수로서 표현할 수 있다는 것을 보았다.
그러나 단순한 형태의 사후 확률이 모든 종류의 클래스 조건부 밀도 분포에 대해 결과로 나오는 것은 아니다.
- 가우시안 혼합 분포를 이용하면 불가능하다.
다른 종류의 판별적 확률 모델을 살펴보도록 한다.
2개의 분류 문제를 가진 일반화된 선형 모델의 틀을 유지한다.
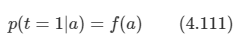
여기서 a=wT ϕ 이고, 함수 f는 활성 함수(activation function)가 된다.
노이즈 임계값 모델을 고려해서 연결 함수를 선택할 수 있다.
ϕn을 an=wTϕn으로 계산한 후, 다음에 따라 표적값을 설정한다.
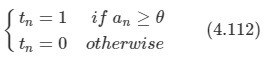
여기서 θ 는 확률 밀도 p( θ )에서 추출된다면 활성 함수는 다음과 같이 기술할 수 있다.


여기서 파란색 곡선은 p( θ )로 두 개의 가우시안 함수의 혼합으로 이루어진다.
이에 해당하는 누적 분포 함수 f(a)는 붉은색 곡선으로 그려져 있다.
파란색 곡선 상의 녹색 수직선에서의 값은 같은 지점에서의 붉은색 곡선의 기울기와 같다.
이제 p( θ )를 표준 정규 분포로 생각한다면 식을 다음과 같이 기술할 수 있다.

이 함수를 역프로빗 함수라고 부른다.
시그모이드 함수의 모양과 비슷하게 생겼으므로 일반적인 가우시안 분포를 사용해도 이 모델은 그대로 유지된다.
오차 함수는 다음과 같이 정의된다.

이 함수는 보통 erf 함수 또는 에러 함수라고 부른다.
- 머신 러닝 모델에서 사용중인 오류 함수와는 다른 것이다.
이 오차 함수는 역프로빗 함수와 다음과 같은 관계를 가진다.

역프로빗 활성화 함수를 바탕으로 한 일반화된 선형 모델을 프로빗 회귀라 한다.
MLE 방법을 이용하여 프로빗 회귀의 매개변수를 구할 수 있다.
- 로지스틱 회귀와 비슷한 경우가 많다.
실제 응용 사례에서 문제가 될 수 있는 것은 outlier이다.
입력 벡터 x를 측정할 때, 오류가 발생하거나 표적 벡터 t를 잘못 라벨링했을 때, 이상값 문제가 발생한다.
이러한 데이터는 분류기를 심각하게 왜곡할 수 있다.
로지스틱 회귀 모델과 프로빗 회귀 모델은 서로 다른 반응을 보인다.
- 로지스틱 모델은 x가 문한대로 감에 따라서 exp(-x)와 같이 감쇠되는 반면, 프로빗은 exp(-x2)와 같이 감쇠되므로 더 예민하게 반응한다.
하지만 두 모델 모두 데이터는 모두 정확하게 라벨링되어 있다고 가정한다.
4.3.6 정준 연결 함수
가우시안 노이즈 분포를 사용한 선형 회귀 모델에서 에러 함수는 음의 로그 가능도 함수를 사용한다.

여기서 매개변수 벡터 w에 대해 미분하면 오륫값에 특징 벡터를 곱한 형태를 띠게 된다.
이 결과가 타깃 변수의 조건부 분포가 지수족에 포함되는 경우에 일반적으로 얻을 수 있는 결과이다.
- 이 경우의 활성화 함수를 정준 연결 함수(canonical link function)라 한다.
입력 벡터 x에 대해 지수족 함수 분포를 가정했지만 여기서는 타겟 값 t에 대해 가정한다.
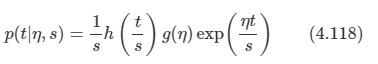
일반화된 선형 모델은 y가 입력의 선형 결합을 비선형 함수에 넣은 결과로 표현되는 모델이라 정의된다.

- 여기서 f()가 활성 함수이며, f-1()가 연결 함수다.
η 의 함수로 표현되는 이 모델의 로그 가능도 함수를 고려해보자.

모든 관측값들이 동일한 척도 매개변수를 공유한다고 가정한다.
- s는 n에 대해 독립적이다.
모델 매개변수 w에 대해 미분하면 다음과 같다.

여기서 an=wT ϕ n이고, yn=f(an)이다.
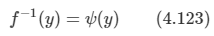
f( ψ (y))=y 이고, 따라서 f'( ψ ) ψ '(y)=1이다.
또한 a=f-1(y) 이므로 a = ϕ 이고, 결국 f'(a) ψ '(y)=1이 된다.
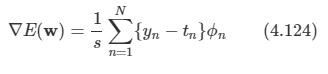
'Book > Machine Learning' 카테고리의 다른 글
| [ML]12. Continuous Latent Variable - part1 (0) | 2020.03.02 |
|---|---|
| [ML]ch 9.Mixture models and EM (0) | 2020.02.24 |
| [ML]ch 4. Linear Models for Classification - part 1 (0) | 2020.02.10 |
| [ML]ch 3. Linear Models for Regression (0) | 2020.02.03 |
| [ML]ch 2. Probability Distributions (0) | 2020.01.27 |