아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
1. 소개(Introduction)
-
패턴인식이란 컴퓨터 알고리즘을 활용하여 데이터의 규칙성을 자동적으로 찾아내고, 이 규칙성을 이용하여 데이터를 각각의 카테고리로 분류하는 등의 일을 하는 분야
-
휴리스틱 알고리즘을 통해 생성된 규칙으로 문제를 해결할 수 있다.
- 각각의 규칙에 대해 예외 사항을 적용해야 하며 이로 인해 수많은 rule을 만들어야 함.

-
머신러닝을 사용하면 더 나은 결과를 얻을 수 있다. 위와 같이 손으로 쓴 숫자를 분류하는 예제가 있다고 하자. 그러면 N개의 숫자들을 training set으로 활용하고, 각 숫자의 카테고리를 표적 벡터로 표현해 매개변수를 조절해 학습한다.
일반화(Generalization)
- 훈련 데이터가 실제 모든 데이터를 대변하지 많는다.
- 따라서 가지고 있는 데이터를 통해 새로운 예시들을 올바르게 분류하는 능력을 일반화(Generalization)이라고 한다. 이는 패턴 인식의 가장 중요한 목표다.
- 입력 데이터를 사전에 정제하는 작업을 진행하는데 이 과정을 통해 문제를 더 쉽게 해결할 수 있다.
- 이 과정을 전처리(preprocessing) 또는 특징 추출(feature extraction) 과정이라고 부른다.
기계 학습의 종류
-
지도 학습(Supervised Learning)
- 주어진 훈련 데이터가 입력 벡터와 그에 해당하는 표적 벡터로 이루어지는 문제
- 분류(classification), 회귀(regression)
-
비지도 학습(Unsupervised Learning)
- 훈련 데이터가 해당 표적 없이 오직 입력 벡터 x로만 주어지는 경우
- 군집화(clustering), 밀도 추정(density estimation)
-
강화 학습(Reinforcement Learning)
-
주어진 상황에서 보상을 최대화하기 위한 행동
-
지도학습과는 다르게 입력값과 최적의 출력 값을 예시로 주지 않음
-
탐험(Exploration)과 탐사(Exploitation) 간의 트레이드오프 문제
-
1.1 Example
실숫값의 입력 변수인 x를 관찰한 후 이 값을 바탕으로 실숫값의 타깃 변수인 t를 예측하려 한다.
- 예제에 사용될 변수를 가정하자.
- N개의 관찰값 x로 이루어진 훈련 집합 x=(x1, x2,... xN)^T, 타깃 변수 t=(t1,..., tN)^T
- tn은 sin(2 pi x)의 출력값에 가우시안 분포만큼의 노이즈를 더해서 만들었음

-
그림에서 녹색 선이 sin(2 pix) 함수이며, 파란색 원이 가우시안 랜덤 분포에 의해 발생한 샘플
- 관측된 값들은 노이즈로 인해 변질되어 있어서 각각의 주어진 x에 대해서 어떤 값이 적합한 t인지가 불확실하다.
- 1.2절에서 진행할 확률론에서 더 자세히 이야기할 것이다.
-
해당 곡선을 fitting 하기 위해서 다음과 같은 형태의 다항식을 활용한다.

- 다항식을 사용한 이유는 추후에 설명하도록 한다.
-
훈련 집합의 표적 값들의 값과 함숫값 y(x, w)와의 오차를 측정하는 오차 함수(error function)를 정의하고 이 함수의 값을 최소화하는 방식으로 피팅할 수 있다.
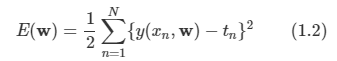
- 위와 같이 오차 함수를 사용하며 각각의 데이터 포인트에 대한 예측치와 해당 표적값 사이의 오차를 제곱하여 합산하는 방식이다. 그리고 1/2는 나중의 편의를 위해서 추가되었다.
-
우리는 E(w)를 최소화하는 w 값을 선택함으로써 이 곡선 피팅 문제를 해결할 수 있다.
- 오차 함수가 이차 다항식의 형태를 지니고 있기 때문에 이 함수를 계수에 대해 미분하면 w에 대해 선형인 식이 나올 것이고, 오차 함수를 최소화하는 유일한 해를 찾아낼 수 있을 것이다.
- 유일한 해 w를 앞으로 w*라고 표현한다.
-
다항식의 차수 M을 결정해야 한다.
- 이 문제를 Model comparison(모델 비교), Model Selection(모델 결정)이라 부른다.
- 차수 M에 따라서 표현되는 곡선이 달라지므로 어떠한 차수를 선택할지는 중요하다.
-
M = 0,1,3,9 인 경우에 대해 다항식으로 피팅하는 예시다.

- M=0 ,1 인 경우에는 함수를 잘 표현하지 못하는 것으로 보인다.
- M=3 인 경우에는 가장 잘 표현하는 것으로 보인다.
- M=9 일 경우에 완벽하게 피팅이 되는 경우로 오차 함수의 값이 0일 것이다.
- 하지만 M=3 인 경우를 선택하는 것이 가장 좋은 선택이다.
- 최종 목적은 새로운 데이터 x가 입력되는 경우에 가장 적합한 결과를 제공하는 일반화 모델을 얻는 것이다.
- M= 9인 경우에는 새로운 데이터에 대해 매우 좋지 못한 성능을 보일 것이다.
-
이처럼 주어진 데이터에 비해 M이 너무 클 경우를 과적합(over-fitting)이라고 하고, 너무 작을 경우를 과소 적합(under-fitting)이라고 한다.
- 과적합은 bias가 작고, variance가 크다고 하며, 과소 적합은 bias가 크지만 variance가 작다고 한다.
- bias와 variance는 트레이드 오프 관계이다.
-
일반화의 성능을 측정할 수 있는 수치가 있으면 편리하다. 따라서 RMS 에러(Root Mean Square error)를 사용한다.

- N으로 나눔으로써 데이터 사이즈가 다른 경우에도 비교할 수 있도록 했고, 제곱근을 취함으로 표적 값과 같은 크기를 가지도록 했다.
- RMS가 작을수록 더 좋은 모델임을 의미한다.
-
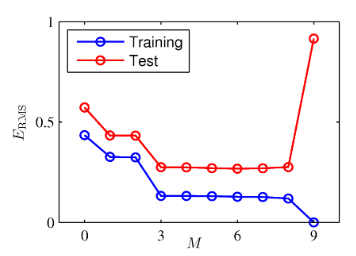
각각의 M에 대해서 RMS의 값을 확인해보면 과적합 되는 지점을 알 수 있다.
- RMS의 값이 M이 커질수록 작아지는 것은 당연하다.
- 대신 M=9처럼 test의 RMS가 급격하게 커지는 구간을 과적합 되는 지점이라고 할 수 있다.
-
데이터의 크기에 따라 모델의 결과가 달라진다.


- 위 그림에서 사용한 M의 값은 9로 동일하며 왼쪽은 N=15, 오른쪽은 N=100의 샘플 크기가 존재한다.
- M=9를 사용했지만 N=100일 경우 과적합의 흔적이 보이지 않는다.
- 즉 과적합 문제는 더 많은 샘플을 확보함으로써 해결할 수 있다.
- 앞으로 최대 가능도(Maximum likelihood), 베이지안(Bayesian) 방법을 사용해 과적합 문제를 해결할 수 있다.
-
정규화(regularization)를 통해 제한적인 양의 데이터 집합을 통해 복잡하고 유연한 모델을 생성할 수 있다.
- 과적합이 발생한다면 w의 값이 매우 커지거나 매우 작아지는 현상이 발생한다. 따라서 이를 막기 위해 패널티 항을 추가하는 방식이다.

- 여기서 ||w||^2 = W^TW 이며, 계수 람다가 정규화항의 제곱합 오류항에 대한 상대적인 중요도를 결정짓는다.
-
람다에 대해서 더 알아보도록 한다.
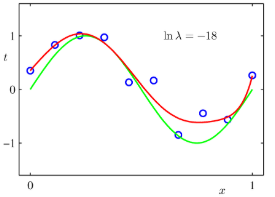

- 그림을 통해 M=9이고 동일한 크기의 샘플 데이터가 적용된 결과에 람다를 추가하면 위와 같은 현상이 발생한다.
- ln 람다 = -18인 경우 과적합이 없어지고 원래 근사하려던 식과 매우 유사해진다.
- 하지만 ln 람다 = 0을 보면 지나치게 큰 람다는 과소적합 현상을 만들어낸다.
1.2 확률론
패턴 인식 분야에서 중요한 것 중 하나는 ''불확실성''이다. 불확실성은 노이즈를 통해서도 발생하고 데이터 집합의 수가 제한되어 있어서 발생하게 된다.
-
확률론(Probability Theory)
- 불확실성을 계량화하고 조작하기 위한 이론적인 토대를 마련해 주며, 패턴 인식 분야의 중요한 기반

-
위 그림의 예시를 통해서 확률론에 대해서 알아보도록 하자.
- 두 개의 상자가 주어지고, 하나는 빨간색 상자, 다른 하나는 파란색 상자라고 하자.
- 빨간색 상자에는 6개의 오렌지, 2개의 사과가 있다.
- 파란색 상자에는 1개의 오렌지, 3개의 사과가 있다.
- 랜덤하게 상자 하나를 골라 임의로 과일 하나를 꺼내고 넣는 작업을 수행하며, 상자 안에서 각각의 과일을 고를 확률을 동일하다.
- 빨간색 상자를 고를 확률은 0.4, 파란색 상자를 고를 확률은 0.6이라고 하자.
- p(B=r) = 4/10, p(B=b) = 6/10
- 이제 '사과를 고를 전반적인 확률은?', '오렌지를 선택했을 때 파란 상자였을 확률은?'과 같은 질문에 답할 수 있어야 한다.
-
이를 위해 확률의 두 가지 기본 법칙은 합의 법칙(sum rule), 곱의 법칙(product rule)에 대해서 알아본다.
-
합의 법칙

-
곱의 법칙
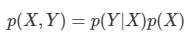
-
위 수식들은 다음과 같은 과정을 통해 얻을 수 있다.


-
X가 xi, Y가 yj 일 확률을 위와 같이 적는다. 이때 Y 값과 무관하게 X가 xi 값을 가질 확률을 구해보자.
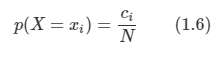
-
이 때 ci = 시그마 nij이다. 이로부터 합의 법칙을 유도할 수 있다.
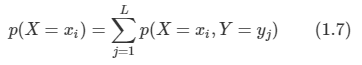
-
곱의 법칙도 비슷하다.

-
1.8의 식을 X=xi일 때, Y=yj일 경우를 의미하며 이를 조건부 확률이라고 한다. 따라서 1.5,1.6,1.8을 통해서 다음 1.9와 같은 관계를 도출할 수 있으며 이것이 바로 곱의 법칙이다.
-
-
-
합의 법칙과 곱의 법칙을 이용하여 베이즈 정리를 기술할 수 있다.(유명한 정리이므로 자세한 설명은 생략한다.)

- 이것을 토대로 사과와 오렌지 예제에 적용하면 다음과 같다.

1.2.1 확률 밀도(probability density)
-
지금까지는 이산적인 사건을 바탕으로 확률에 대해 알아보았다면 이번에는 연속적인 변수에서의 확률에 대해 알아보도록 한다.

-
위와 같이 표현되는 것을 확률 밀도(probability density)라고 부른다.
-
확률은 양의 값을 가지고 x의 값은 실수에 존재해야 한다. 따라서 확률 밀도 함수는 아래 두 조건을 만족시켜야 한다.

-
x에 대해 확률 함수 p(x)가 주어졌을 때 구간 (-무한, z)에 대한 확률 값을 누적 분포 함수(cumulative distribution function)라고 한다.
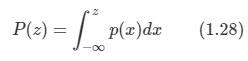
-
위 그림을 보면 이해하기 쉬우며, P(x)를 미분하면 p(x)를 얻을 수 있다.
-
1.2.2 기댓값과 공분산(Expectation and covariance)
-
확률식에서 주어진 데이터에 대한 무게 중심을 구하는 것은 매우 중요한데, 주로 평균(기댓값)이 사용된다.
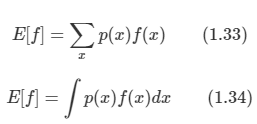
-
이산 분포, 연속 분포에 일 때의 기댓값을 구하는 방법이다.
-
간혹 여러 개의 변수를 사용하는 함수에 대해 평균값을 표기할 경우가 있다,
-
이 때는 평균에 사용하는 주변수에 대해 기술한다.

-
f(x, y)의 평균값을 x의 분호에 대해 구하라는 의미이다.
-
-
-
f(x)의 분산은 다음과 같이 정의된다.

-
분산은 f(x)가 평균값 E [f(x)]로부터 전반적으로 얼마나 멀리 분포되어 있는지를 나타내는 값이다. 위 식을 전개하면 f(x)와 f(x)^2의 기댓값으로 표현할 수도 있다.

-
2개의 랜덤 변수 x와 y에 대해 공분산은 다음과 같이 정의된다.
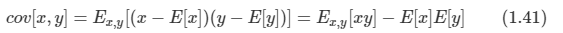
-
x와 y가 서로 독립이라면 공분산 값은 0이 된다.
-
1.2.3 베이지안 확률
- 지금까지 확률을 ''반복 가능한 임의의 사건의 빈도수''라는 측면에서 봄. 이러한 해석을 고전적 혹은 빈도적이라고 한다.
-
베이지안 관점을 사용하면 확률을 이용해서 불확실성을 정량화하는 것이 가능하다.
- 베이지안 관점은 확률의 개념을 빈도가 아닌 믿음의 정도로 고려하는 것
-
앞에서 말했던 예제인 곡선 피팅 문제를 다시 생각해보자. 이 문제에서 w가 알려지지 않은 고정된 값으로 여겨졌는데 베이지안 관점을 적용하면 w에 대한 불확실성을 기술할 수 있다.

-
이 식은 관측하기 전의 w에 대한 가정을 p(w)로 표현을 하고 w의 불확실한 정도를 수식에 반영하고 있다.
-
p(w)는 모수에 대한 사전 확률 분포를 의미
-
p(w|D)는 D를 관측한 후의 w에 대한 불확실성을 사후 확률로 표현
-
p(D|w)는 가능도 함수(likelihood function)이라고 불리며, 각각의 다른 매개변수 벡터 w에 대해 관측된 데이터 집합이 얼마나 '그렇게 나타날 가능성이 있었는지'를 표현
-
최종적으로 다음과 같은 식을 만들 수 있다.

-
식 1.43의 양쪽 변을 w에 대해 적분하면 베이지안 정리의 분모를 사전 확률과 가능도 함수로 표현할 수 있다.
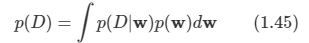
-
-
-
더 자세한 내용은 2장에서 살펴보도록 한다.
1.2.4 가우시안 분포
2장에서 다양한 확률 분포와 각각의 성질에 대해 살펴볼 것인데, 가우시안 분포에 대해 간단히 개념을 살펴보고 간다.
-
가우시안 분포는 두 개의 매개변수 u와 시그마^2에 의해 통제된다. u는 평균, 시그마^2은 분산이며, 분산의 제곱근 값은 표준 편차라 불린다. 또한 분산의 역에 해당하는 값은 정밀도라고 한다.
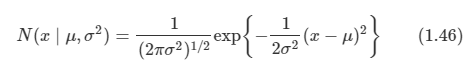

-
가우시안 분포를 정규 분포라고도 부르며 다음과 같은 성질들이 있다.
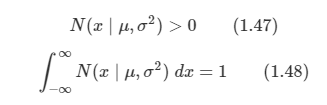
-
모든 값에서 0보다 큰 값을 가지고 전체 합은 1이라는 특징은 정규화의 특징으로써 가우시안 분포가 정규화되어 있음을 알 수 있다.

- 가우시안 분포의 기댓값과 분산은 위와 같다.
- 하나의 관찰 데이터 집합 x=(x1, x2, x3,..., xN) T이 주어졌다고 하자. 그러면 데이터 집합 하나가 관찰될 수 있는 확률은 얼마일까?
-
같은 분포에서 독립적으로 추출된 데이터 포인트들을 독립적이고 동일하게 분포(i.i.d) 되었다고 한다.
-
따라서 각 사건의 주변 확률의 곱으로 표현이 된다. 따라서 조건부 확률로 다음과 같이 적을 수 있다.

-
이것을 그림으로 나타내면 다음과 같다.
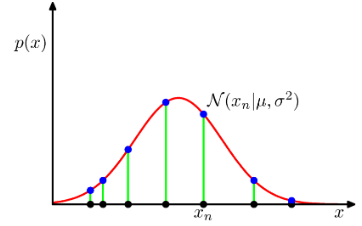
-
-
실제로 얻는 것은 관찰 데이터 집합이고 이를 이용하여 원래의 가우시안 분포를 결정하는 문제를 풀어야 한다.
-
즉 주어진 샘플이 어떠한 특징을 가지고 있는 가우시안 분포에서 나왔는지를 찾으라는 이야기이며, 평균과 분산의 값을 구하면 된다.
-
따라서 식 (1.53)의 가능도 함수를 최대화하는 방식으로 평균과 분산을 찾으면 된다.
-
로그 함수는 변수에 대해 단조 증가하는 함수이므로 로그를 취한 후 최댓값을 찾을 수 있다. 이 점이 분석이 간단해지고 수치적인 측면에서도 도움이 되기 때문이다.

-
-
이 함수의 해는 다음과 같다. 각각의 표본 평균, 표본 분산이라고 부른다.

1.2.5 곡선 피팅
-
이전에는 다항식 곡선 피팅 문제를 오차 최소화 측면에서 살펴보았는데, 이번에는 확률적 측면에서 살펴본다.
- 이를 통해 오차 함수와 정규화에 대한 통찰을 얻을 수 있다.
- 베이지안 해결법을 도출하는데 도움이 될 것이다.
-
곡선 피팅 문제의 목표는 가지고 있는 샘플 데이터들로 새로운 입력 변수가 주어졌을 때 그에 대한 타깃 변수를 예측해 내는 것이다.
-
따라서 확률 분포를 이용해 타깃 변수의 값에 대한 불확실성을 표현할 수 있다. 노이즈를 가우시안 분포로 고려하면 다음과 같이 표현할 수 있다.

-
B는 정밀도 매개변수를 의미한다. 이를 그림으로 표현하면 아래와 같다.

-
즉 한 점이 주어지고 그 점을 중심으로 가우시안 노이즈가 존재하는 것과 같다.
-
-
훈련 집합을 바탕으로 최대 가능도 방법을 이용하여 파라미터들을 결정할 수 있다. 가능도 함수는 다음과 같다.
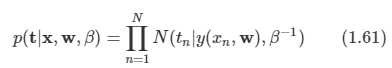
-
로그를 취하고 이 가능도 함수를 최대로 만드는 파라미터 값을 추정한다.

-
MLE를 이용해 얻어진 해 w를 wML로 표기를 하며 마지막 두 term은 w에 관계없으니, 제거, 계수의 B/2도 1/2로 바꿀 수 있다. 마지막으로 로그 가능도를 최대화하는 대신에 로그 가능도의 음의 값을 취한 후, 이를 최소화하면 제곱항 오차 함수를 유도할 수 있게 된다.

-
위와 같은 방식으로 새로운 데이터의 타겟 값을 예측할 수 있으며 이를 예측 분포라고 한다.

-
베이지안 방식을 위해 다항 계수 w에 대한 사전 분포를 도입한다.

-
여기서 a는 분포의 정밀도이며, M+1은 M차수 다항식 벡터 w의 원소의 개수다. a와 같이 모델 매개변수의 분포를 제어하는 변수들을 하이퍼 파라미터(hyperparameter)라고 한다.
-
베이즈 정리를 이용하면 다음과 같이 식을 쓸 수 있다.
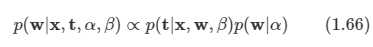
-
이제 주어진 데이터에 대해 가장 가능성 높은 w를 찾는 방식으로 w를 결정할 수 있다. 즉, 사후 분포를 최대화하는 방식으로 w를 결정할 수 있다. 이 방식을 최대 사후 분포(MAP maximum posterior)라 한다.

-
1.2.6 베이지안 커브 피팅
-
아직 w에 대해 점 추정을 하고 있기 때문에 아직은 완벽한 베이지안 방법론을 구사한다고 말할 수 없다. 완전한 베이지안적 접근을 위해 모든 w에 대한 값을 반영해야 한다. 따라서 모든 w에 대해 적분을 시행하게 된다.

-
적분을 시행하면 다음과 같이 가우시안 분포로 주어진다.
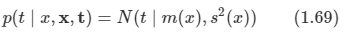
-
여기서 평균은 다음과 같다.

1.3 모델 선택
-
지금까지 최소 제곱법을 이용하여 곡선 피팅의 예시에서 최적의 다항식 차수가 있음을 알 수 있었다.
- 다항식의 차수에 따라 자유 매개변수의 수가 결정되며, 모델의 복잡도가 결정되었다.
- 정규화 계수도 복잡도에 영향을 주었다.
- 실제 응용 사례에서는 이러한 매개변수의 값을 결정해야 하며, 가장 적합한 모델을 선택해야 한다.
-
대부분의 경우에는 train과 test에 대한 데이터의 공급이 제한적이다. 이런 상황에서 해결할 수 있는 한 가지 방법이 교차 검증법 (cross-validation)이다.
-
임의로 고른 (S-1)/S를 학습 집합으로 나머지를 테스트 집합으로 사용한다. S를 번갈아가면서 N번 테스트한다.
-
S의 수가 늘어나면 모델 훈련의 시행 횟수가 증가하게 된다. 이는 훈련이 계산적으로 복잡할 때 문제가 된다.
-
여러 가지 복잡도 매개변수가 있을 경우 기하급수적인 수의 훈련 실행이 필요할지도 모른다.
-
이상적인 방식에서는 훈련 집합만을 활용해서 여러 종류의 하이퍼파라미터와 모델의 비교를 한 번의 훈련 과정 동안 시행할 수 있다.
-
이를 위해 훈련 집합만을 사용하는 성능 척도가 필요하며, 과적합으로 인한 bias로부터 자유로워야 한다.

-
'Book > Machine Learning' 카테고리의 다른 글
| [ML]ch 4. Linear Models for Classification - part 1 (0) | 2020.02.10 |
|---|---|
| [ML]ch 3. Linear Models for Regression (0) | 2020.02.03 |
| [ML]ch 2. Probability Distributions (0) | 2020.01.27 |
| [ML]ch 1. Introduction-part 2 (0) | 2020.01.20 |
| [ML]chapter 0. Beginning (0) | 2020.01.13 |