아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
4. 선형 분류 모델
- 지금까지는 회귀 문제에 대해서만 다루어 보았지만 이번엔 분류 문제에 대해서 다루어 보도록 한다.
- 분류는 입력 벡터 x를 받았을 때 대응되는 클래스에 속하도록 하는 작업이다.
- 이 때 클래스는 K개로 Ck 로 표기한다.
- 하나의 데이터는 하나의 클래스에만 속하며, 하나의 클래스는 다른 클래스를 포함하지 않는다.
- 이렇게 나누어진 영역을 decision region이라고 부르며 나누는 경계면을 decision boundaries라고 부른다.
4.1 판별 함수
4.1.1 두 개의 클래스
- 선형 판별식의 가장 간단한 형태를 다음과 같다.

- 여기서 w는 가중치 벡터라 부르고, w0은 bias라고 부른다. 회귀랑 동일하다.
-
보통 2개의 클래스를 분류하는 문제에서 y(x)>=0인 경우를 C1으로 분류하고, 아닌 경우를 C2로 분류한다.
- 이 때 decision boundaries는 y(x)=0임을 알 수 있다.
-
이제 임의의 두 점 xA, xB가 이 경계면 위에 있다고 하자.
-
이 때 y(xA)=y(xB)=0를 만족하고, wT(xA−xB)=0다. 여기서 w는 결정 경계에 대해 수직임을 알 수 있다.
-
결정 경계에서 식을 전개하면 다음의 식을 얻을 수 있다.
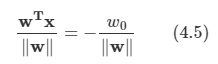
-
-
이제 D=2라고 할 때 그림을 살펴본다.

- 임의의 한 점 x에 대해 결정 경계면에 수직으로 내린 지점을 xㅗ라고 하자.
-
이 경우 다음과 같은 식이 성립한다.

-
3장에서와 비슷하게 x0=1를 이용하자.
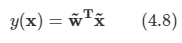
- 위와 같이 간단하게 적을 수 있다.
4.1.2 다중 클래스
-
K > 2인 상황을 다중 클래스라고 부른다.
- 이 문제를 2-class 문제를 여러 개 조합해서 해결할 수 있다.
- K-1개의 2-class 분류기가 있으면 K개의 클래스를 분류 가능하다.

- 왼쪽 그림을 보면 3개의 클래스를 분류하기 위해 2개의 2-class 문제를 사용하였다. 하지만 녹색 영역과 같이 판정을 할 수 없는 부분이 생기게 된다.
-
또한 만약 K(K-1)/2 개의 분류기를 사용해서 분류를 한다면 오른쪽과 같다.
- 이 경우에도 녹색 영역과 같은 애매한 부분이 생긴다.
-
이 문제를 해결하기 위해 다른 방법을 사용한다.
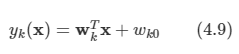
-
j != k일 때, yk(x)>yj(x)를 만족하면 x를 클래스 Ck로 판별하자.
-
그러면 두 클래스 간의 decision boundaries는 yk(x)=yj(x)에서 형성된다.
-
이 때 식을 전개하면,
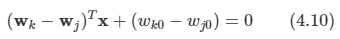
-
2-class 문제에서 사용하던 것과 같다.
-
-
이러한 판별 함수의 결정 경계는 언제나 단일하게 연결되어 있으며 볼록 성질을 가진다.
-
모두 하나의 선으로 연결되어 있고, 내부의 어느 각도 180도를 넘지 않는다는 것과 같다.
-
이를 확인할 수 있다.

-
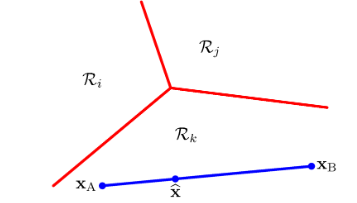
xA,xB는 같은 지역의 임의의 두 점이다. x는 두 점 사이에 위치한 임의의 한 점을 나타내고, λ 는 0과 1 사이의 값이다.

-
yk(xA)>yj(xA) 이고 yk(xB)>yj(xB)이므로 yk(xˆ)>yj(xˆ)가 된다. 즉 아래 그림과 같다.
-
-
4.1.3 분류를 위한 최소 제곱법
-
최소제곱법을 사용해서 분류 문제를 해결해보자.
- 사실 그리 정확하진 않다.
-
판별식은 다음과 같이 정의하고 간단히 정리하는 것이 가능하다.
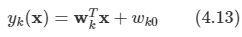
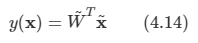
-
n번째 행이 tnT인 행렬 T와 n번째 행이 x
nT라 하면, 전체 샘플 데이터를 X로 정의할 수 있다.
-
최소제곱법을 다음과 같이 적는다.

-
Tr은 행렬의 trace를 의미하며, trace는 행렬의 대각성분 합을 의미한다.
-
W에 대해 미분하고 정리하면 다음과 같다.

-
X† 는 pseudo-inverse 행렬이다.
-
-
모든 훈련 집합의 표적 벡터들이 식 4.18의 선형 제약 조건을 어떠한 a와 b 값에 대해서 만족한다면 x 값에 대한 모델 예측값이나 제약 조건 4.19를 만족한다.


-
원 핫 인코딩을 통해 얻은 예측값들은 어떤 x의 경우에든 y(x)의 원소들을 전부 합하면 1이 된다.
- 하지만 (0,1) 범위 내 안이라는 조건은 없으므로 확률값이라고 할 수 없다.
-
문제는 최소 제곱법은 outlier에 대해 너무 민감한 성질을 보인다. 따라서 더 강건한 모델을 고를 필요가 있다.

- 녹색선은 로지스틱 회귀 분석으로 얻은 경계선, 보라색 선은 최소 제곱법을 사용한 것이다.
- 보라색선은 우측의 그림처럼 outlier가 존재할 때 잘 분류하지 못하는 것을 알 수 있다.
4.1.4 피셔의 선형 판별
- 2-class 문제로 접근을 한다.
-
D차원의 입력 벡터 x를 일차원에 투영한다고 해보자. 식은 다음과 같다.

-
이 식은 임의의 한 벡터를 한 차원의 벡터 위의 한 점(스칼라 값)으로 변환해준다.
- y에 임계값을 추가해 클래스를 분류하도록 한다.
-
높은 차원을 낮은 차원으로 줄였기 때문에 정보 손실은 당연하다.
- 그렇기 때문에 정보 손실을 적게 하도록 해야 한다.
-
w에 투영되었을 경우에 클래스 간의 분리 정도를 측정할 수 있는 가장 쉬운 방법은 투영된 클래스의 평균들이 얼마나 분리되어 있는가를 보는 것이다.
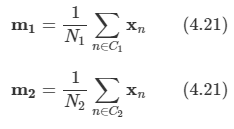
- 각 클래스의 평균을 나타내는 벡터를 표기할 수 있다.
- 이 값을 가지고 두 클래스간의 거리가 최대화되도록 하는 식을 전개한다.
-
1차원의 벡터로 투영된 후의 값은 다음과 같다.
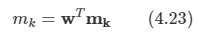
- w를 찾아야 하는데, w 값만 무한정 커지면 값이 커지므로 단위 벡터로 고정을 한다.
- 이 식에 라그랑주 승수법을 적용해서 최소값을 구하면 w는 (m2-m1)에 비례한다.

- 왼쪽이 지금까지 한 방법인데 상당히 중복되는 것을 볼 수 있다. 이는 클래스 분포가 심한 비대각 공분산을 가지고 있기에 생긴다.
- 피셔의 제안은 투영된 클래스 평균 사이의 분리 정도를 크게 하는 동시에 각 클래스 내의 분산을 작게 하는 함수를 최대화함으로써 클래스 간의 중복을 최소화하는 것이다.
-
따라서 분산도를 정의한다.

-
여기서 yn=wTxn이다. 이 식은 투영 후 점들의 분산도를 의미한다.

-
최종 피셔 판별식은 위와 같으며, 정리하면 다음과 같은 식을 얻게 된다.

-
SB는 클래스 간 공분산 행렬을 의미하고, SW는 클래스 내 공분산 행렬을 의미한다.
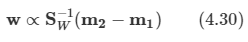
-
J(w)를 w에 미분하면 최종적으로 위와 같은 식을 얻게 된다.
-
4.1.5 최소 제곱법과의 관계
-
에러 함수를 정의해본다.

-
E는 w0와 w에 대해 각각 미분하고 그 값을 0으로 설정하면 다음의 식을 얻게 된다.

-
tn은 다음과 같다.
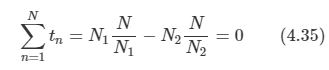
- N1,N2은 각 클래스에 속한 샘플 수를 의미하고 N은 전체 샘플 수를 의미한다.
- C1 = N/N1, C2=N2
-
m은 전체 데이터 집합의 평균이다.

-
4.32식에 xn을 곱하고 전개하면 다음과 같다.

-
최종적으로 다음과 같으면 피셔 판별식과 동일하다.

4.1.6 다중 클래스에 대한 피셔 판별식
-
이제 K의 값이 2보다 큰 경우 피셔 판별식을 적용해보자.
- 단 K<D임을 가정하자.
-
D차원을 더 낮은 차원으로 변환하는 식을 아래와 같이 기술한다.

- W의 컬럼 개수는 D'로 정의한다. 당연히 D'의 값은 D보다 작다.
-
클래스 내 공분산 행렬
-
앞서 살펴본 SW를 K개의 클래스 버젼으로 확장한다.
-
Nk는 클래스 Ck에 속한 샘플의 수 이다.
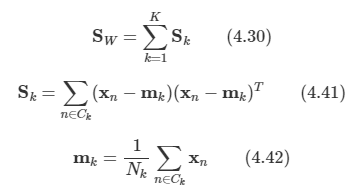
-
-
클래스 간 공분산 행렬
-
클래스 사이의 분산이 아닌 전체 데이터에 대한 공분산 행렬을 정의한다.
-
N은 전체 샘플 합계 : N=sum to k Nk
-
m은 전체 평균

-
이 때 클래스 간 분산과 클래스 내 분산으로 나눌 수 있다.
-
즉, ST로 부터 SW를 제외한 나머지를 S B라고 정의한다.

-
이 공분산 행렬들은 x 공간상에서 정의되었다. 행렬들을 투영된 D'차원의 y 공간상에서 정의해보자.

-
에러 함수 만들 때, 여러 가지 선택지가 있지만 Fukunaga의 방법을 선택한다.

-
투영 행렬 W에 대한 명시적인 함수로 다음과 같이 다시 적는다.

- 이 기준을 최대화 하는 것은 어렵지 않지만 노력이 필요해서 Fukunaga에 설명되어 있다고 한다.
-
4.1.7 퍼셉트론 알고리즘
-
2-class에 대해 간단하게 알아보자.
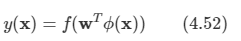
-
활성 함수로 가장 간단한 형태인 계단형 함수를 쓴다.

-
여기서 ϕ 0(x) = 1 이다. 표적값은 0,1 이 아닌 +1, -1로 정의해서 사용한다.
-
퍼셉트론에서 매개변수 w를 구하기 위한 알고리즘도 오류 함수를 최소화하는 방식이다.
-
오분류된 패턴의 총 숫자를 오류 함수로 고를 수 있지만 사용하지 않는다.
- 학습 알고리즘이 복잡해진다.
- 오류 함수가 w에 대해 조각별 상수 함수다. w에 대한 변화가 결정 경계를 데이터 포인트들 중 하나를 건너 이동하게 하는 곳에서 불연속성이 발생한다.
- 따라서 이 경우에 함수의 기울기를 통해서 w를 변경시키는 방법을 사용할 수 없다.
-
따라서 퍼셉트론 기준이라는 오류 함수를 사용한다.

-
-
클래스 C1에 대해서는 wT ϕ (xn) > 0이 되고, C2는 wT ϕ (xn) < 0 을 만족하는 w를 찾고자 한다.
-
에러를 최소화 하는 방향으로 식을 전개해야 하므로 기울기 방법으로 w를 만들 수 있다.

- η : 파라미터 학습 비율
- τ : 알고리즘 스텝 인덱스
-
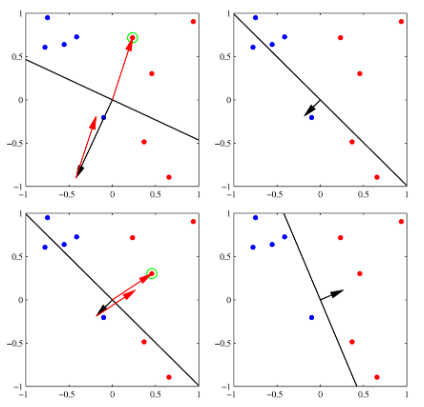
퍼셉트론의 동작 방식을 잘 설명하고 있는 그림이다.
- 녹색 점이 오분류된 점인데 그에 따라 빨간색 방향만큼 보정이 된다.
- 보정을 하고 난 뒤 다시 오분류된 점을 찾아 보정을 하는 작업을 계속해서 거치면 결정 경계가 완성된다.
-
아래 식을 통해 업데이트를 진행하면 에러가 점점 줄어든다는 것을 알 수 있다.

-
퍼셉트론 수렴 법칙(Perceptron convergence theorem)
- 정확한 해를 가지고 있기만 한다면 퍼셉트론 학습 알고리즘은 정확한 해를 유한한 단계 안에 확실히 구할 수 있다.
- 훈련 집합이 선형적으로 분리가 가능해야 한다.
- 하지만 수렴을 위해 필요한 단계의 수가 매우 많을 수 있다.
- 분리가 불가능한 문제인지, 단순히 수렴하는 데 오랜 시간이 걸리는 문제인지 구별이 불가능
- 정확한 해를 가지고 있기만 한다면 퍼셉트론 학습 알고리즘은 정확한 해를 유한한 단계 안에 확실히 구할 수 있다.
-
퍼셉트론은 출력 값이 확률 값이 아니다.
-
중요한 제약 중 하나는 고정된 기저 함수의 선형 결합을 기반으로 한다.
'Book > Machine Learning' 카테고리의 다른 글
| [ML]ch 9.Mixture models and EM (0) | 2020.02.24 |
|---|---|
| [ML]ch 4. Linear Models for Classification - part 2 (0) | 2020.02.17 |
| [ML]ch 3. Linear Models for Regression (0) | 2020.02.03 |
| [ML]ch 2. Probability Distributions (0) | 2020.01.27 |
| [ML]ch 1. Introduction-part 2 (0) | 2020.01.20 |