문제:
N x M 크기의 배열로 표현되는 미로가 있다.
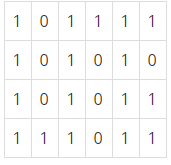
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1,1)에서 출발하여 (N,M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
입력:
첫째 줄에 두 정수 N,M(2<=N,M<=100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력:
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
풀이방법:
최소의 칸 수를 구해야 하는 문제에서는 DFS가 적합하지 않은 경우가 많다. 따라서 이 문제는 BFS를 사용해서 풀어야 하는 문제다.
BFS(queue)를 사용해서 1이 있는 위치에다가 check에 거리를 할당하며 (1,1)에서 (N,M)으로 가도록 하면 된다. 예제 입력2를 통해 설명하면 다음과 같다.
초기 check 배열은 다음과 같이 모두 0이며 (1,1)에서 출발해야 하므로 0,0은 1으로 할당해두도록 한다. 또한 (1,1)를 queue에 넣어두도록 한다.
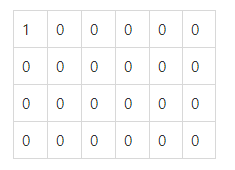
queue에서 (1,1)을 빼고 이 값을 기준으로 (1,2)와(2,1)가 1로 이동할 수 있으므로 2로 할당한다. 이 값들을 queue에 넣어준다.
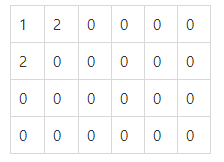
(1,2)와 (2,1)를 빼고 이 값에서는 (2,2),(1,3)이 이동 가능하므로 3으로 할당하고 이 값들을 queue에 넣어준다.
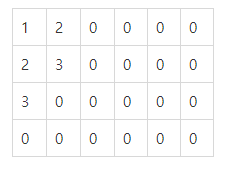
따라서 이 방식대로 계속해서 queue에서 빼고, 넣는 작업을 반복한다
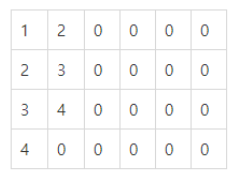
count=5일 때,
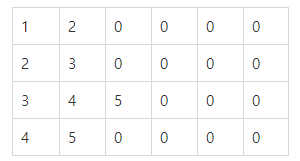
count=6일 때,
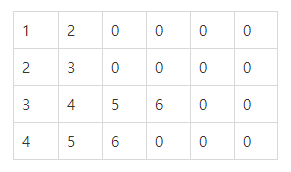
count=7일 때,
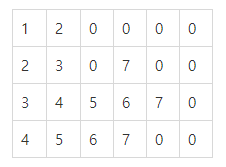
count=8일 때,
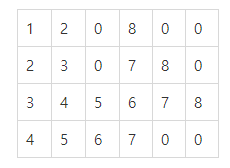
count=9일 때,
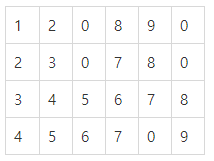
이렇게 계속하다보면 더 이상 queue에 남아 있는 값이 없게 되는데 이 것이 탐색의 끝을 의미한다. 따라서 탐색을 마치고 난 뒤에 (n,m) 값이 정답이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
import queue
n,m=map(int,input().split())
miro=[]
dx=[0,0,1,-1]
dy=[1,-1,0,0]
for i in range(n):
miro.append(list(map(int,list(input()))))
check=[[0 for i in range(m)]for j in range(n)]
q=queue.Queue()
q.put((0,0))
check[0][0]=1
temp=queue.Queue()
count=2
while q.qsize():
x,y=q.get()
for i in range(4):
newX=x+dx[i]
newY=y+dy[i]
if 0<=newX<n and 0<=newY<m:
if miro[newX][newY]==1 and check[newX][newY]==0:
temp.put((newX,newY))
check[newX][newY]=count
if q.qsize()==0:
q=temp
count+=1
temp=queue.Queue()
print(check[n-1][m-1])
|
cs |
문제링크:
'Algorithm > Python' 카테고리의 다른 글
| [BOJ]1371. 가장 많은 글자 (0) | 2019.09.10 |
|---|---|
| [BOJ]9933. 민균이의 비밀번호 (0) | 2019.09.09 |
| [BOJ]2667. 단지번호붙이기 (0) | 2019.09.07 |
| [BOJ]2331. 반복 수열 (6) | 2019.09.06 |
| [BOJ] 10451.순열 사이클 (0) | 2019.09.05 |