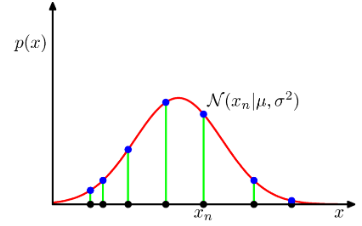
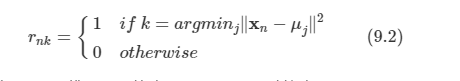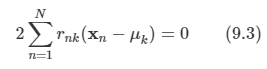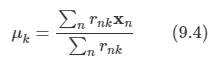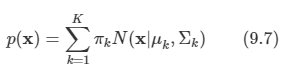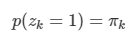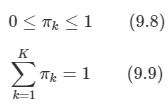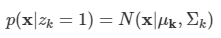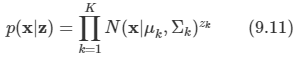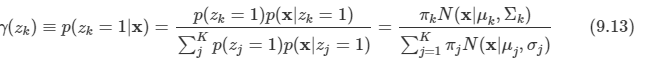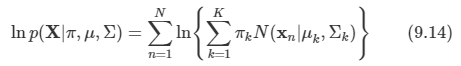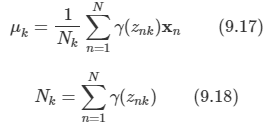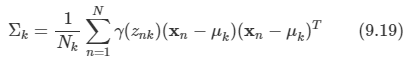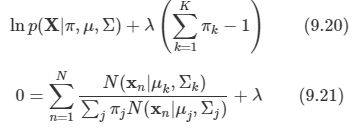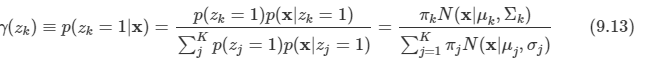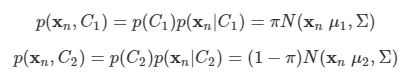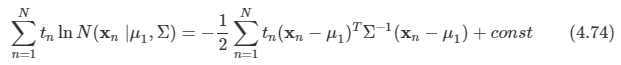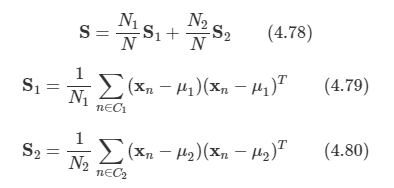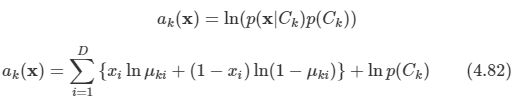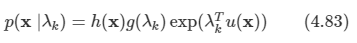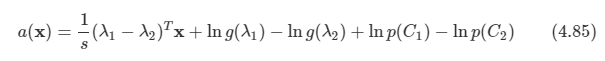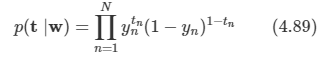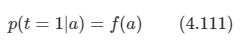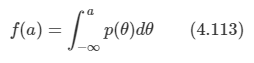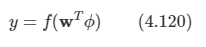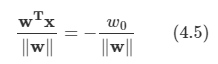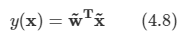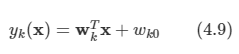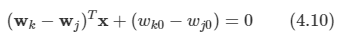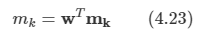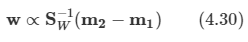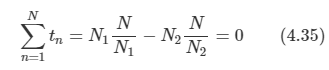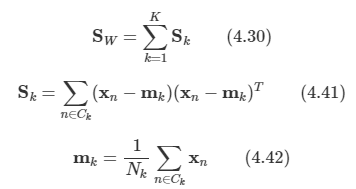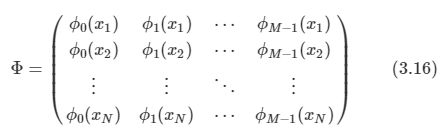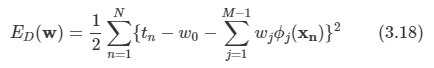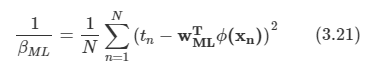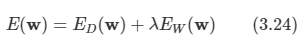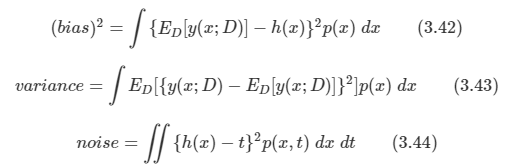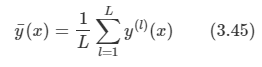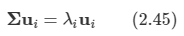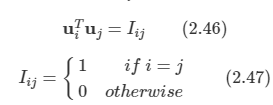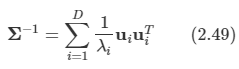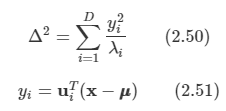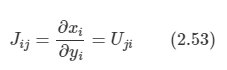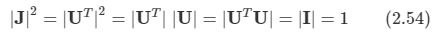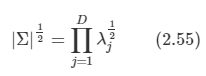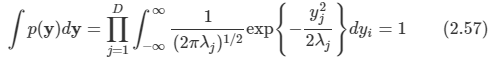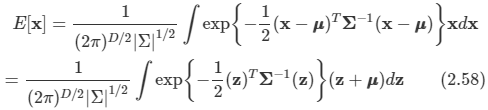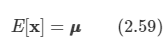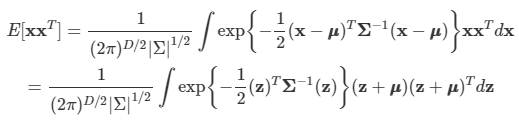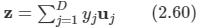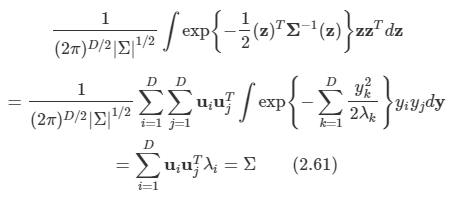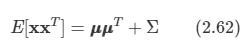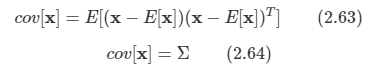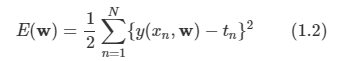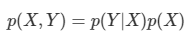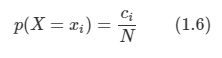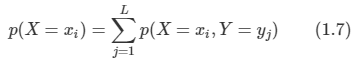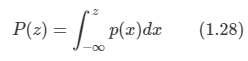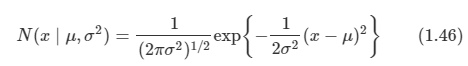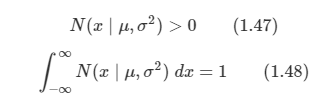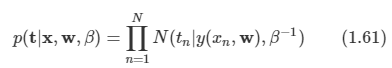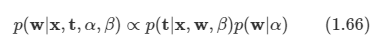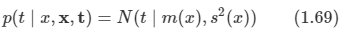아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
12. 연속 잠재 변수
이미 9장에서 가우시안 혼합 분포와 같은 이산 잠재 변수를 가지는 확률 모델을 살펴보았다.
- 이제 몇몇 잠재 변수들 또는 모든 잠재 변수들이 연속적인 모델에 대해 살펴본다.
이러한 모델은 원래 데이터 집합 공간의 차원보다 훨씬 더 낮은 차원의 manifold에 모든 데이터 포인트들이 가깝게 놓이는 성질을 가진다.
- manifold란 데이터가 있는 공간이라고 생각하면 된다.
예시를 살펴 보도록 한다.
64 x 64 픽셀로 표현되는 숫자 이미지를 100 x 100 크기의 이미지에 삽입하도록 한다.
빈 공간은 0 값을 가지게 되고, 숫자를 넣는 위치는 random이며 다음과 같이 표현된다.

각 이미지는 10,000개의 픽셀을 가지게 되며, 세 개의 변동 가능한 자유도만이 존재한다.
- 수직 이동, 수평 이동, 회전 이동
각각의 데이터 포인트들은 실 데이터 공간의 부분 공간상에 존재, 이 부분 공간을 intrinsic dimensionality라고 한다.
위의 예시의 경우 manifold는 비선형이다. 하나의 숫자를 이동시켰을 때 특정 픽셀은 0에서 1로, 다시 0으로 바뀌는 비선형 이기 때문이다.
또한 이동과 회전 매개변수는 잠재 변수들이다.
- 우리가 관측하게 되는 것은 이미지 벡터인데 생성될 때 이동 변수나 회전 변수들이 사용되었는지 알 수 없다.
가장 단순한 연속 잠재 변수 모델에서는 잠재 변수와 관측 변수가 둘 다 가우시안 분포를 이룬다고 가정하고 잠재 변수들의 상태에 대한 관측 변수들의 선형 가우시안 종속성을 사용한다.
- 이를 통해 PCA를 도출한다.
12.1 PCA
PCA는 차원수 감소, 손실 허용 데이터 압축, 특징 추출, 데이터 시각화 등의 여러 분야에서 사용되고 있다.
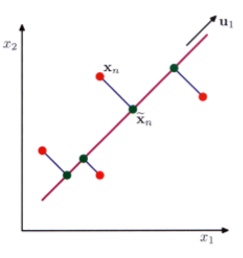
- PCA에는 두 가지 정의가 있지만 결과적으로는 같은 알고리즘을 도출하게 된다.
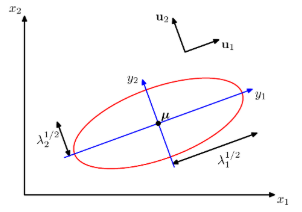
- 데이터를 주 부분 공간(prinipal subspace)이라고 하는 더 낮은 선형 공간에 직교 투영하는 과정이며 위 그림과 같이 진행된다.
- 이때 투영 과정은 투영된 데이터의 분산이 최대화되는 방향으로 이루어져야 한다.
- 평균 투영 비용을 최소화하는 선형 투영으로 PCA를 정의
- 이 경우 평균 투영 비용은 데이터 포인트와 그 투영체 간의 평균 제곱 거리로 정의
- 데이터를 주 부분 공간(prinipal subspace)이라고 하는 더 낮은 선형 공간에 직교 투영하는 과정이며 위 그림과 같이 진행된다.
12.1.1 최대 분산 공식화
- 관측 데이터 집합 xn이 있다고 하자. 이는 차원수 D를 가지는 유클리드 변수다. 우리의 목표는 데이터를 M < D의 차원수를 가지는 공간상에 투영하는 것이다.
- 이때 투영된 데이터의 분산이 최대가 되도록 한다.
- M값이 주어졌다고 가정하고, 나중에 적절한 M 값을 찾아내는 것을 알아본다.
- M = 1이라고 하자.
- 이 공간의 방향을 D차원 벡터 u1로 정의할 수 있다. 편의를 위해서 단위 벡터를 사용한다.
- 즉 u1Tu1 = 1 이다.
- u1에 의해 정의되는 방향이므로 임의의 크기를 자기는 벡터를 사용해도 일반성을 잃지 않는다.
- 즉 u1Tu1 = 1 이다.
- 각각의 데이터 포인트는 u1Txn에 투영된다.

그리고 투영된 데이터 분산은 다음처럼 주어진다.

S는 데이터 공분산 행렬로서 다음처럼 주어진다.
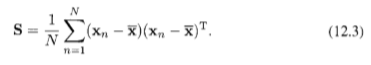
이제 투영된 분산을 u1에 대해서 극대화하도록 한다. 이 때 이 값이 무한대로 발산하는 것을 막기 위해 제약 조건을 걸어야 하며 정규화 조건으로부터 제약 조건을 얻고 라그랑주 승수법을 도입해 최대화를 실시하도록 한다.
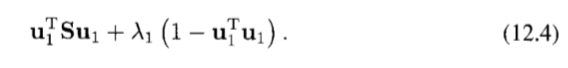
u1에 대한 미분을 0으로 설정하면 다음과 같다.

즉 u1이 S의 고유 벡터가 된다. 왼쪽에 u1T를 곱하면 분산은 다음과 같이 주어진다.
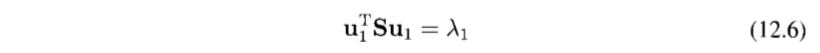
u1를 가장 큰 고윳값 λ1을 가지는 고유 벡터로 설정하면 최대의 분산을 가지게 되고, 이 고유 벡터를 제1주성분이라고 한다.
요약하면, PCA는 데이터 집합의 평균과 공분산 행렬 S를 계산하고 S의 가장 큰 M개의 고윳값들에 해당하는 M개의 고유 벡터들을 찾는 과정
12.1.2 최소 오류 공식화
투영 오류를 최소화하는 방식을 살펴본다.
완전히 정규 직교하는 D차원의 기저 벡터들 ui을 도입해 보자.
- uiTuj = δij를 만족한다.
이 기저들은 완전하므로, 데이터 포인트들을 기저 벡터들의 선형 결합으로 정확하게 표현할 수 있다.
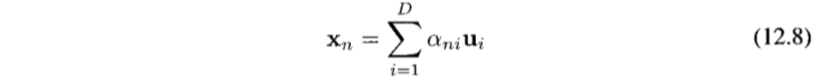
계수 ani는 각 데이터 포인트마다 다른 값이며, 새 시스템으로 좌표계를 회전 변환하는 것에 해당한다.
uj와 내적을 진행한 후 정규 직교 성질을 이용하면 anj=xnTuj를 얻는다.

목표는 이 데이터 포인트들을 제한된 수 M < D개의 변수들을 이용해서 근사하는 것
- 저차원 부분 공간으로의 투영에 해당
M개의 기저 벡터들을 이용해 M차원 선형 부분 공간 표현할 수 있고, xn을 다음과 같이 근사한다.
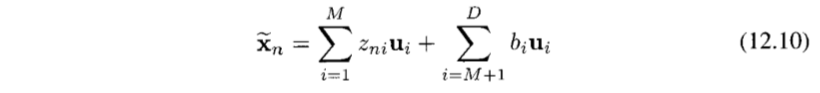
zni는 특정 데이터 포인트에 대해 종속적이지만 bi는 모든 데이터 포인트들에 대해 동일한 상수다.
- 이러한 값들은 차원을 줄임으로 인해 발생하는 왜곡도를 감소시키는 방향으로 자유롭게 선택할 수 있다.
왜곡도를 측정하고 이를 최소화하도록 한다. 왜곡도는 다음과 같다.
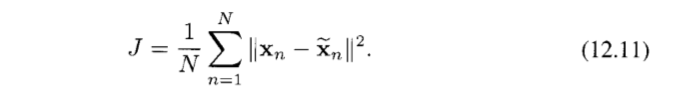
우선 각각의 zni 값에 대한 최소화를 고려해 보자. x_tilda 값을 치환하고, znj에 대한 미분값을 0으로 설정한 후 정규직교 조건을 사용하면 다음을 구할 수 있다.

- 여기서 j = 1, ... ,M이다.
- 12.10 식에서 앞 부분에 해당하는 것을 의미한다.
bi에 대한 미분값을 0으로 놓고 정규직교 조건을 이용하면 다음을 얻을 수 있다.

- 여기서 j = M+1, ... , D다.
- 12.10 식에서 뒷 부분에 해당하는 것을 의미한다.
여기서 zni와 식 12.10의 bi를 대입해 넣고 식 12.9의 일반 전개식을 사용하면 다음과 같다.

이로부터 xn에서 x_tilda로의 이동 벡터는 주 부분 공간에 직교하는 공간상에 존재함을 알 수 있다.
- 이동 벡터들은 i = M+1 , ... , D에 대한 {ui}의 선형 결합이기 때문
- 투영된 포인트는 x_tilda 부분 공간상에 놓여 있어야 하지만, 공간 내에서는 자유롭게 이동시킬 수 있으므로 최소 오류를 달성 할 수 있다.
따라서 J를 {ui}의 함수로 표현한다.

이제 {ui}에 대해 최소화한다.
- 이는 제약 조건이 있는 최소화이다. 따라서 라그랑주 승수법을 사용한다.
- 제약 조건은 정규직교 조건으로부터 기인한다.
이차원 데이터 공간 D = 2, 주 부분 공간 M = 1의 예시로 살펴본다.
J=u2TSu2를 최소화하는 방향 u2를 선택해야 하고, 제약 조건u2Tu2=1을 만족해야 한다.
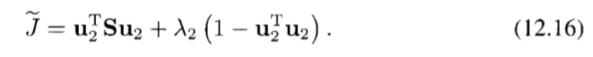
u2에 대한 미분값을 0으로 설정하면 Su2 = λ2u2를 얻는다. u2는 S의 고유 벡터가 된다.
u2에 대한 해를 왜곡도 식에 역으로 대입해 넣으면 J=λ2가 된다.
- 두 개의 고윳값들 중 작은 고윳값에 해당하는 고유 벡터로 u2를 선택해 J를 최소로 만들 수 있다.
이 내용은 제곱 투영 거리의 평균값을 최소화하기 위해 주성분 부분 공간이 데이터 포인트들의 평균을 통과하도록 해 최대 분산의 방향과 정렬되도록 한다.
따라서 이를 일반화하면 다음과 같다.

지금까지는 M < D인 경우만 고려하였는데, M=D인 경우에도 유효하다.
- 이 경우엔 차원 감소는 없으며, 좌표축들을 회전시켜 주성분들에 정렬되도록 한다.
'Book > Machine Learning' 카테고리의 다른 글
| [Machine Learning]1. Introduction- part.2 (0) | 2022.03.02 |
|---|---|
| [Machine Learning]1. Introduction- part.1 (0) | 2022.02.17 |
| [ML]ch 9.Mixture models and EM (0) | 2020.02.24 |
| [ML]ch 4. Linear Models for Classification - part 2 (0) | 2020.02.17 |
| [ML]ch 4. Linear Models for Classification - part 1 (0) | 2020.02.10 |