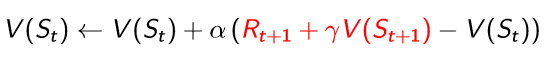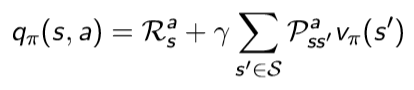CodeDrive

Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

6. Value Function Approximation

지금까지는 Grid World를 통해서 작은 상황을 설정했고 table로 저장하는 것이 가능했다. 그리고 value function과 policy를 구하는 과정을 살펴보았다. 이러한 문제들을 Tabular Method라고 부른다. 하지만 실제 문제에 대해서 강화학습을 적용하기에는 너무 크다.

지금 강화학습으로 해결할 수 있거나 해결하려고 하는 문제에 대해서 state의 갯수를 알아보면 다음과 같다. Backgammon은 10²⁰, 알파고는 10¹⁷⁰, 헬리콥터(자율주행)은 사실상 무한대의 상태들을 가지고 있다. 따라서 이러한 문제에 대해서 value function과 policy를 구하고자 하는 것은 어렵다. 따라서 이 값들을 추정하는 방법들에서 배우도록 한다.

function approximation을 하는 방법은 어렵지 않다. 새로운 변수 w를 대입해서 이 변수가 table의 정보를 대변하도록 만들면 된다. 즉 다음과 같이 함수화 할 수 있다.

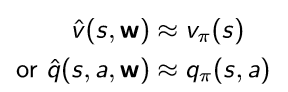
w는 학습을 통해서 update하며, true value와 근사하도록 맞춰나간다. 최근에는 이 학습을 하는 과정에 deep learning을 사용하기도 한다.

Value Function Approximation에는 다음과 같은 종류들이 있다고 한다.

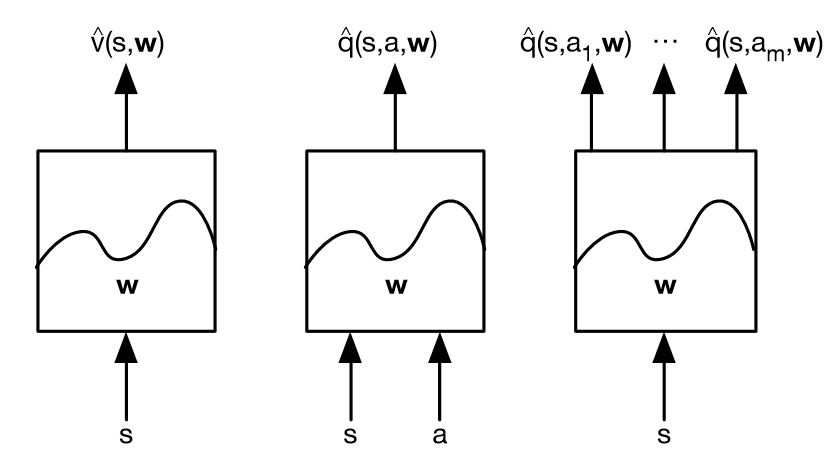
function approximator에는 여러 개가 있지만 그 중 미분가능한 Linear combinations of features, Neural network를 이번 장에서 소개하도록 한다. 그리고 이들은 non-stationary, non-iid한 data라고 하는데, 분포가 계속해서 바뀌며 독립적이지 않다.

Incremental Methods

w를 업데이트를 하는 방법중 가장 좋은 것은 Gradient Descent이다. 이 방법은 간단하고 프로그램 상으로도 강력하다. 하지만 시작점에서 조금만 달라져도 다른 점에 도착할 수 있고, 이 점이 local optima일 수도 있다.

w로 표현되는 loss function인 J(w)는 true value와의 error로써 이를 최소화하는 것이 목적이다.

이를 미분해서 값을 update 할 수 있는데 expectation을 쓰는 방법과 sampling을 하는 방법이 있고 다음과 같다.

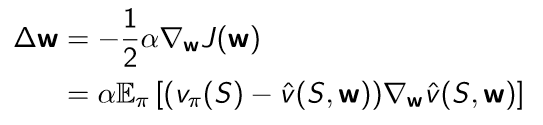
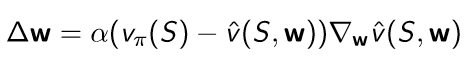
MC와 TD에서 했던 것처럼 v_π(S)를 대체해서 사용할 수 있다.

MC with Value Function Approximation

MC의 G_t는 unbiased 하고, true value의 noisy sample이다. 그러므로 training data를 지도학습으로 적용할 수 있다. 그래서 위와 같이 사용가능하며, local optimum으로 수렴하게 된다. 그리고 non-linear한 경우에도 적용할 수 있다고 한다.

TD Learning with Value Function Approximation

TD-target은 guess를 사용하는 것이기 때문에 true value의 biased sample이다. 하지만 여전히 training data를 지도학습으로 적용이 가능하고 위에서 소개한 것처럼 TD(0)를 적용할 수 있다.

Linear TD(0)는 (거의) global optimum에 수렴한다.

TD(λ) with Value Function Approximation

G_t^λ도 true value의 biased sample이다. 그러므로 역시 training data를 지도학습으로 적용할 수 있으며 Forward view linear TD(λ), Backward view linear TD(λ)로 각각 적용할 수 있고, 서로 equivalent하다.

Control with Value Function Approximation

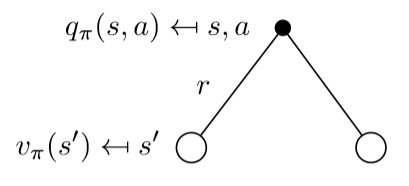
하지만 value function을 사용하면 control 문제를 다룰 때 발생했던 model-free가 발생한다. 따라서 이번에도 value function을 q-function으로 바꾸도록 한다.

그리고 그 뒤로는 value function을 했던 내용과 동일합니다.

Batch Methods

Gradient descent는 간단하고 매력적이지만 한번 쓰고 버린다. 따라서 sample efficient하지 않다고 한다. 따라서 Batch method는 1000개의 데이터가 있으면 그 중 10개를 sample로 해서 사용하는 방식이다. 이를 통해 value function의 best fitting을 찾을 수 있다고 한다.

value function approximation을 사용하고, experience D는 <state, value>의 쌍으로 구성된다. 이 때 best fitting value인 파라미터 w를 찾기 위해서 Least squares 알고리즘을 사용한다.

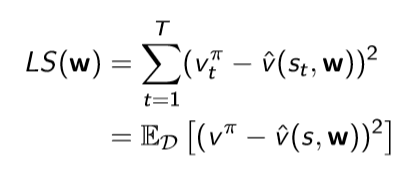
Least squares 알고리즘은 추측값과 참값 사이의 sum-squared error를 최소화하는 w를 찾는 알고리즘이다.

Stochastic Gradient Descent with Experience Replay

<state, value>로 쌍이 묶어진 experience D가 있을 때, 다음을 반복한다.

그러면 이는 다음과 같이 수렴한다.

이러한 방법을 Experience replay라고 하며 강화학습에서 자주 사용하는 방법이다.

Experience replay in Deep Q Networks

Non-linear랑 off-policy일 때 학습을 진행하면 수렴을 하지 않고 발산한다는 문제점이 발생한다. 따라서 이러한 문제를 해결하기 위해 DQN은 experience replay와 fixed Q-target을 사용한다고 한다.

• Experience reaply: 어떤 action에 어떤 reward와 그 state등 정보들이 있는 transition을 replay memory에 저장하고, random하게 mini batch를 뽑는다. 그리고 MSE를 통해 학습한다.
• Fixed Q-target: target을 계산할 때에 예전 parameter를 쓰는 것, 두 개의 파라미터 set이 있다. 하나는 고정시키고 다른 하나는 업데이트 중인 파라미터 set을 가진다. non-linear 함수일 때에 업데이트 방향이 계속 바뀌기 때문에 수렴되기 어렵다. 따라서 1000번 정도는 고정된 parameter set을 사용하며 진행하다가 그 이후에 고정된 parameter set을 업데이트 하던 parameter set으로 바꾼다. 예전 버전을 w^-, 현재 버전을 w라 했을 때, target에서는 고정된 것을 사용하기 때문에 fixed Q-target이라 한다.

Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

5. Model Free Control

• Model Free : MDP에 대한 정보가 없는 경우, 즉 environment에 대한 정보를 가지고 있지 않다.
• Control : value function을 최적화 하는 것, 즉 최적의 정책을 찾는 것

Model Free Control에서는 다양한 예제들이 있으며, 주로 다음 특징을 가지는 문제들을 해결한다,

• MDP를 모르지만, 경험을 sampling 할 수 있다.
• MDP는 알지만, sample들을 제외하고는 사용하기에는 너무 크다.

On Policy & Off Policy

• On Policy learning
  • "Learn on the job"
  • 학습하는 policy와 행동하는 policy가 같은 경우
    • ex)Sarsa
• Off Policy learning
  • "Look over someone's shoulder"
  • 학습하는 policy와 행동하는 policy가 반드시 같지 않아도 된다.
    • ex)Q-learning

On-Policy Monte-Carlo Control

• Generalised Policy Iteration

  

  • 3장에서 배웠던 내용으로 최적의 정책을 찾는 문제를 해결하기 위한 일반적인 방법론이다.
    • 임의의 정책으로 시작하여 value function을 추정하는 단계를 거친다.
    • 추정한 value를 바탕으로 정책을 발전시킨다.
    • 다시 맨처음으로 돌아간다.
    • 이는 EM 알고리즘과 같은 형태를 가지고 있다.
      • 따라서 Policy evaluation을 E단계, Policy improvement를 M 단계라 지칭한다.

• 4장에서 value function을 estimate 하는 방법들에 대해서 배웠는데 이를 E 단계에 적용해보도록 한다.

  • 하지만 그대로 적용한다면 다음과 같은 3가지 문제가 발생하게 된다.
    1. Value funcion의 model-based
    2. Local optimum
    3. Inefficiency of policy evaluation

1. Model-based

MC로 E단계를 수행하게 된다면 state value function을 사용해야 한다. 하지만 value function을 사용하면 M단계를 진행할 때 문제가 발생하게 된다. MC를 사용했던 이유가 Model-Free이기 때문이지만 value function으로 policy를 improve하려면 MDP의 model을 알아야 한다.

즉 위와 같이 reward와 state transition probaility를 알아야 한다. 즉 Model-based이어야 한다는 것이다.

따라서 이를 해결하기 위해서 value function을 action value function으로 바꾸게 되면 Model-Free 성질을 만족할 수 있다.

• return이 아닌 agent가 episode마다 random하게 움직이며 얻은 reward들 그리고 state transition prob.를 통해서 action-value function을 계산할 수 있다.

2. Local optimum

그러면 이제 Policy evaluation에서 value function을 action value function으로 바꾼다면 On policy MC를 사용할 수 있는 것일까? 다음 예시를 살펴보도록 한다.

• 두 개의 문이 내 앞에 있다.

  • 처음 왼쪽 문을 열었고, reward 0을 받았다.

    • V(left) = 0

  • 두번째에는 오른쪽 문을 열었고, reward 1을 받았다.

    • V(right) = +1

  • 세번째에 오른쪽 문을 열었고, reward 3을 받았다.

    • V(right) = +2

  • 네번째에 오른쪽 문을 열었고, reward 2를 받았다.

    • V(right) = +2

  • 그러면 지금까지 상황을 보았을 때 어느 문을 여는 것이 최선의 선택일까?

    • 아마도 이 네가지 상황으로만 본다면 오른쪽 문을 여는 것이 최선의 선택으로 보인다. 하지만 다음에 왼쪽 문을 열었을 때 reward를 100을 받을 수도 있는 것이다. 즉 지금 탐험과 탐사 trade-off에 빠지게 된 상황이다.

  • exploration(탐험) : environment에서 더 많은 정보를 알아내고자 하는 방법으로, 모든 행동을 할 때 일정 확률로 다른 곳으로 이동한다.

  • exploitation(탐사) : 알고 있는 정보를 바탕으로 보상을 최대화하고자 하는 것이다.

즉 지금 greedy 하게 improve 하는 것은 탐사에 빠지게 되는 것이다. 따라서 탐험을 어느정도 보장함으로써 model을 모르는 상황에서 더 좋은 성능을 낼 수 있을 것이다.

따라서 policy를 최적화 할 때 다음과 같이 일정한 확률을 부여해서 정하도록 한다.

3. Inefficiency of policy evaluation

하지만 MC 방법의 경우에 모든 episode들을 다 마친 후에 evaluation을 하면 너무 오랜 시간이 걸린다는 단점이 존재하게 된다. 따라서 이를 줄이기 위해서 매 episode들이 끝난 후에 policy evaluation을 수행하는 것으로 바꾸도록 한다.

즉 최종적인 On-Policy Monte-Carlo Control은 다음과 같다.

On- Policy Temporal-Difference Learning

TD가 MC보다 적은 variance를 가지고 online으로 학습가능하며, Incomplete sequence라는 장점들을 가지고 있기 때문에 control 문제에 적용해볼 수 있다.

Prediction에서 TD는 다음과 같이 표현을 했었다.

MC와 같은 이유로 value function을 사용할 수 없으므로 해당되는 부분들을 action value function으로 수정하도록 하자. 따라서 S에서 A 행동을 하면 보상 R을 받고 S'이라는 상태로 이동한다. 이 상태 S'에서 A'이라는 임의의 행동을 할 때의 action value function 값이 필요한 것이므로 다음과 같이 표현할 수 있다.

따라서 이를 앞부터 철자를 따서 Sarsa라고 부른다. Policy evaluation 부분에 MC 대신에 sarsa를 적용하면 다음과 같다.

n-step Sarsa

Sarsa가 애초에 TD의 개념에서 나온 것이므로 TD(λ)와 마찬가지로 Sarsa(λ)로 사용할 수 있다.

• forward view Sarsa(λ)

  • MC와 TD의 절충안이 n-step인 것처럼, 여러 개의 n-step을 선택하여 이의 평균을 취하면 각 n-step의 장점을 모두 가질 수 있게 된다. 이 때, 단순히 산술평균을 사용하는 것이 아니라 λ라는 weight를 이용해서 가중 평균을 취하도록하고 이를 Forward-view라고 한다.

  • episode가 모두 끝나야 계산이 가능하다. 따라서 TD의 장점을 많이 잃게 된다.

    

• backward view sarsa(λ)

  • 이제는 다시 forward-view TD(λ)에서 time-step마다 update할 수 있는 방법을 알아본다. 여기서 eligibility trace라는 개념이 나오게 된다. 이는 과거에 방문했던 state 중에서 현재 얻게 되는 reward에 영향을 주는 state를 판단해, 현재 얻게 되는 reward를 해당 state에 나누는 것이다.

    

Off- Policy learning

자신의 policy가 아니라 다른 사람의 policy를 통해서 학습을 하는 것이다. 이는 다음과 같은 관점으로 인해 중요하다.

1. 다른 agent를 관찰하는 것으로부터 배운다.
   • 다른 사람의 policy를(행동을) 따라 하는 것이 아닌, 경험만을 받아 학습해서 새로운 행동을 한다.
2. On policy의 경우에는 경험을 통해 policy를 업데이트를 했다면 사용한 경험은 버린다. 하지만 off policy는 이를 버리지 않고 재사용한다.
3. 탐험적인 행동을 하면서 최적의 policy를 찾을 수 있다.
4. 한 policy를 따르면서 여러 개의 policy를 학습할 수 있다.

Importance Sampling

X는 확률분포 P상에서 sampling 되는 것이고, Q는 P와 다른 확률분포를 의미한다. f(X)는 모든 함수를 넣을 수 있다. (f(X)=x, f(X)=3x...) 따라서 P를 따를 때의 f(X)의 기댓값을 구하고 싶은 것이다. 그런데 이를 이용해서 Q를 사용했을 때의 기댓값을 구하고 싶은 것이다.

이는 확률 분포 P와 Q의 비율을 곱해서 얻을 수 있는 것이다. 이를 Monte-Carlo에 적용해보자.

• Importance Sampling for Off-Policy Monte-Carlo

  • Monte Carlo를 수행할 때, 지나온 모든 행동들에 대해서 비율을 곱해준다.

  • 하지만 µ가 0이면 되면 사용할 수 없고, variance가 엄청 크기 때문에 사실상 사용할 수 없다.

• Importance Sampling for Off-Policy TD

  • 따라서 MC의 단점을 보완하기 위해서 TD를 사용하도록 한다.

Q-learning

Importance learning을 하지 않으면서 off-policy를 사용하기 위한 방법이다. 다음 행동은 behavior policy로 고르고, 다음 state S'에서 action A'은 target policy를 통해서 선택하는 것이다. 즉 다음과 같이 q-function이 업데이트가 된다.

Off-policy control with Q-learning

Q-learning에서는 behavior policy와 target policy를 동시에 improve 할 수 있다. Q-learning에서는 behavior policy μ는 ε-greedy로 target policy π는 greedy하게 선택하도록 한다. 각각 수렴 속도가 느리고, local optima에 빠질 수 있다는 단점을 해결하기 위해 적용된 절충안이다.

따라서 이제 다음과 같이 Q-learning이 진행된다.

1. 현재 state S에서 behavior policy μ( ε-greedy)에 따라 action A를 선택한다.

2. q-function을 이용해서 다음 state S'에서의 action A'은 π(greedy)에 따라 선택한다.

   

3. Q-learning의 target은 다음과 같이 구한다.

4. 다음과 같이 최종 update를 수행한다.

   

Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

Model Free Prediction

• Model Free : MDP에 대한 정보가 없는 경우, 즉 environment에 대한 정보를 가지고 있지 않다.

• Prediction : value function을 학습하는 것

즉 Model Free Prediction은 MDP에 대한 정보가 없을 때 value function을 학습해야 하는 문제이고, 다음 장에서 Model Free Control에 대해서 알아보도록 한다.

이번 강의에서 소개한 Model Free Prediction 방법으로 크게 Monte-Carlo Learning(MC), Temporal-Difference Learning(TD)가 있다.

Monte-Carlo Learning

몬테 카를로 방법(다음 부터 MC라 부른다.)은 episode들로 부터 직접적으로 학습한다. 즉 모두 종료가 되는 episode들의 return의 평균을 통해서 학습을 진행한다는 것이다. 그러므로 MC는 완전한 episode들로 부터 학습을 하며 이를 no bootstrapping(추측치로 업데이트 하기)이라고 부른다.

• Goal : Prediction 문제이므로 policy는 π로 정해져 있고, 이를 통해 나온 episode들을 통해 vπ 를 학습하는 것

• return은 Gt=Rt+1+γRt+2+ ... + γT−1RT 와 같이 정의 했으며 vπ(s) = Eπ [Gt | St = s] 로 정의했었다.

MC 방법은 state들을 방문한 것을 바탕으로 다시 크게 First와 Every로 나뉘게 된다.

First- Visit MC Policy Evaluation

terminate까지 도달하기 위해서 state들을 여러번 방문할 수 있는데, , 이때 해당 state에 처음 접한 후 얻은 return 값의 평균을 사용하여 구한다.

Every-Visit MC Policy Evaluation

First와는 달리 state들을 방문할 때마다 return을 계산하고 이를 평균을 내는 방식이다. 보통 first-visit을 사용한다고 한다.

Incremental mean

평균을 구하는 식은 다음과 같이 현재의 값을 뺀 평균의 식으로 바꿀 수 있게 된다. 이를 통해 incremental update를 할 수 있게 된다.

따라서 이를 이용해서 MC 방법에서 V를 계산하는데 사용할 수 있다.

N(S)는 episode를 수행한 횟수에 해당하며 에피소드를 수행하고 나서 v(s)를 바로바로 추정가능하게 된다.

non-stationary 문제의 경우에는 평균을 낼 때 이전의 횟수를 사용하는 것이 아니라 일정한 값인 a로 고정해서 계산을 한다.

Temporal-Difference Learning(TD)

TD방식도 episode들로 부터 직접적인 경험을 하면서 학습을 하는 알고리즘이며 model-free에서 사용한다. 하지만 MC와는 다르게 episode들이 완전히 끝나지 않아도 학습이 가능하며 DP에서 사용하던 bootstrapping 방법을 사용한다. 즉 MC방법과 DP 방법을 적절히 조합한 아이디어라고 할 수 있다. 그리고 추측치에서 다음 추측치를 추정함으로써 업데이트가 가능하다.

MC vs TD

MC와 TD에서 가장 다른 부분은 return Gt이다. MC에서는 종료가 된 episode들로 부터 학습을 하기 때문에 정확한 Gt값을 알 수 있다. 하지만 TD는 그렇지 않기 때문에 return Gt를 추정한 값을 사용해야 한다. 따라서 TD(0)이라고 가정했을 때(뒤에서 이 용어에 대해 자세히 설명한다.),Gt 에 해당하는 부분을 Rt+1+γV(St+1)로 바꿔서 사용하도록 한다.

• 빨간색 term을 TD target이라고 부르고, a 뒤에 있는 항을 TD error라고 부른다고 한다.

TD는 final outcome이 나오기 전에 학습을 할 수 있지만 MC는 결과가 나올 때까지 기다려야 한다. 하지만 TD는 바로바로 학습을 하지만 이 episode가 실제로 종료될 것이라는 보장이 없고, MC는 애초에 끝난 결과를 가지고 학습하므로 확실히 종료된다는 보장을 가지고 있게 된다.

Bias/Varaince Trade-off

v가 실제 Gt에 대해서 unbiased하다고 하면 TD target도 unbiased하다고 할 수 있다. 하지만 TD target은 추정치인 V(St+1)를 사용하기 때문에 bias가 생길 수 밖에 없다.

대신 TD target은 하나의 step에서 계산을 하기 때문에 작은 variance를 가지게 된다. 반면 MC는 episode가 어떤 state sequence로 이루어졌는가에 따라서 value function이 달라지기 때문에 variance가 높게 된다.

즉 종합해보면 MC는 높은 variance를 가지지만 bias가 아예 존재하지 않는다.(정확히 구해진 값들을 사용하기 때문에) 따라서 좋은 수렴 조건을 가지고 있으며, 초기값에 영향을 받지도 않는다.

TD는 낮은 variance를 가지고 있지만 bias가 생기게 된다. 보통 MC보다 더 효과적이고 TD(0)은 수렴을 하지만 항상 그렇다고 볼 순 없다. 또한 초기값에 영향을 받게 된다.

Batch MC and TD

MC, TD 방식 모두 episode를 무한하게 반복하면 실제 value에 수렴할 수 있다. 하지만 batch 방식으로 유한한 episode들을 가지고 학습을 하면 어떻게 될까?

위 예시를 통해서 살펴보도록 한다. 이 예시에서는 8개의 episode들이 있고, 첫번째 episode에서는 A가 reward 0을 받고, B로 가서 reward 0을 받게 된다. 2~7번째 episode들에서는 B에서 reward 1을 받고, 마지막엔 0을 받게 된다.

즉 위 내용을 종합해보면 A는 100% 확률로 B로 가게 될 것이고 이 때 return은 0이 될 것이다.

그러므로 MC에서는 A는 1번 episode에서만 나타나고 이 때 최종 보상이 0이기 때문이다. TD에서는 다른 episode들이 진행이 되면서 A의 value도 같이 업데이트가 될 것이다.

MC는 최종적으로 완료한 episode들의 보상을 사용해서 학습을 하므로 V(A) = 0이 되었다. TD(0) 방식은 max likelihood Markov 방식을 사용하여 수렴하는 알고리즘이기 때문에 V(A) = 0.75가 된다.

이를 보아 TD는 MDP 특성을 가지는 알고리즘이므로 MDP 환경에서 더 유용하고, MC는 그렇지 않기 때문에 MDP가 아닌 환경에서 더 유용하게 된다.

다음은 backup과 bootstrapping에 따른 RL의 분류이다.

TD(λ)

지금까지 설명한 TD들은 TD(0)에 해당하는 것들이었다. 이제 이를 확장해서 TD(λ)로 사용하도록 한다. TD는 guess로 guess를 예측하는 것인데, λ는 steps들에게 얼만큼의 가중치를 부여할지에 대한 값이다. 즉 수식으로 표현하면 다음과 같다.

n=1에 해당하는 것이 우리가 지금까지 보았던 TD(0)에 해당한다. n=2는 G⁽²⁾t와 같이 표현이 될 것이다. 그리고 n이 무한대까지 간다면 이는 종료가 될 때까지 진행한다는 것과 같으므로 MC와 같아지게 된다.

따라서 적당한 n을 잘 선택할 수 있으면 TD와 MC의 장점을 모두 취할 수 있게 된다.

n step에서 n을 고르는 방법은 크게 두 가지 방법이 있다.

• Forward-view TD(λ)

  • MC와 TD의 절충안이 n-step인 것처럼, 여러 개의 n-step을 선택하여 이의 평균을 취하면 각 n-step의 장점을 모두 가질 수 있게 된다. 이 때, 단순히 산술평균을 사용하는 것이 아니라 λ라는 weight를 이용해서 가중 평균을 취하도록하고 이를 Forward-view라고 한다.

    

• Backward-view TD(λ)

  • 이제는 다시 forward-view TD(λ)에서 time-step마다 update할 수 있는 방법을 알아본다. 여기서 eligibility trace라는 개념이 나오게 된다. 이는 과거에 방문했던 state 중에서 현재 얻게 되는 reward에 영향을 주는 state를 판단해, 현재 얻게 되는 reward를 해당 state에 나누는 것이다.

  • 이 때, 영향을 준 것 같은 idx를 credit이라고 하고, 이 credit을 배정할 때 다음 두 개를 사용한다.

    • Frequency heuristic, Recency heuristic

Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

3. Planning by Dynamic Programming

• Model Free : environment에 대한 정보를 가지고 있지 않을 경우
• Model Based : environment에 대한 모델이 있는 경우
  • 이러한 경우에 대해서 Planning, Dynamic Programming을 사용한다.

Introduction

• What is Dynamic Programming?

  알고리즘 문제 기법에서 사용하는 DP, 동적 계획법과 같은 뜻을 가지고 있다. 복잡한 문제에 사용하는 방법으로써 문제를 여러 subproblem으로 쪼갠 뒤에 이 문제를 해결하고 합쳐가면서 풀어가는 방식이다.

  • 다음과 같이 두 가지 특성을 가지는 문제에 대해서 DP를 사용하는 것이 일반적이다.
    • Optimal substructure
      • Optimal한 해는 subproblems들로 분해될 수 있다는 것이다.
    • Overlapping subproblems
      • Subproblem 들이 많이 사용되어서 이를 저장해두었다가 사용할 수 있다.
  • MDP는 위 두 가지 속성을 가지고 있으므로 DP를 사용할 수 있다.
    • Bellman equation은 재귀적으로 분해가 가능하고, value function은 해를 저장하고 재사용할 수 있도록 한다.

• Planning by Dynamic Programming

  DP는 MDP의 모든 것을 알고 있다고 가정한다. 즉 Planning 문제를 해결하는 것이다.

  DP는 크게 두 가지 방법으로 나뉘게 된다.

  • Prediction
    • value function을 학습하는 것
    • MDP, policy가 있을 때 그 policy를 따를 경우의 value function이다.
    • policy evaluation 문제
  • Control
    • optimal 한 policy를 찾는 문제
    • MDP만 있고 optimal 한 policy를 찾아야 한다.
    • policy Iteration, value Iteration

Policy Evalutation

주어진 policy를 평가하는 문제, 이 policy를 따라 간다면 return을 얼마 받는가. 즉 value function을 찾는 문제

초기 value 값을 랜덤하게 초기화 한 후 Bellman Equation을 이용해서 다음 상태 s'를 이용해서 각각의 상태 s의 value 값을 반복적으로 업데이트 한다. 이 때 synchronous backup을 사용한다.

Example

위와 같이 계속해서 반복하다보면 정책이 수렴하는 것을 알 수 있다.

Policy Iteration

위와 같이 반복적인 업데이트를 통해서 모든 상태 s에 대해 value 값을 구할 수 있다.(Evaluate) value 값이 최대가 되는 방향으로 greedy하게 행동하면 초기에 만들었던 Random한 Policy를 개선된 Policy로 만들 수 있다.(Improve) 위와 같은 예시에서는 금방 최적의 Policy로 찾아가는 것을 알 수 있다.

따라서 일반적인 경우에는 Policy를 evaluation해서 value들을 구하고, 그 value들을 바탕으로 Policy를 improvement하는 방향으로 발전시키면 된다.

그런데 과연 greedy 하게 정책을 개선시키는 것이 성능을 항상 좋게 만들까?

다음과 같은 이유들로 항상 그렇다고 하며, 수렴을 하는 포인트는 optimal 하다고 한다.

• Modified Policy Iteration

  하지만 꼭 수렴할 때까지 계속해서 반복해서 진행해야 하는가? 에 대한 의문을 가질 수 있다. 실제로 무한히 반복해서 수렴할 때까지 진행을 하지 않고, k번을 반복해서 그 점을 사용해도 충분히 합리적으로 사용할 수 있다고 한다.

Value Iteration

Value Iteration은 Policy Iteration과는 다르게 Bellman Optimal Equation을 이용하는 것이다.

• Deterministic Value Iteration
  • subproblem의 solution을 알면 Bellman Optimal Equation을 이용해서 s에서의 solution을 알 수 있다.
  • 이러한 반복을 계속해서 한다.
• 아래는 위의 Grid world의 Value Iteration을 적용한 것이다.

• 반복해서 진행하면 세번째 iteration에서 converge 하는 것을 알 수 있다.

Summary of DP Algorithms

*Youtube에 있는 David Silver의 Reinforcement Learning 강의를 보고 작성하였습니다.

Markov Decision Process을 지난 강의에서 배웠던 내용으로 설명하면, 강화학습을 위해 환경을 완전하게 알고 있는 것을 의미한다. 즉 full observable해야 한다. 이러한 이유로 RL의 거의 모든 문제는 MDP로 설계가 되어 있고, MDP하지 않다면 MDP하도록 조건을 더 추가시켜줘야 한다.

Markov Property

이전 강의에서 잠시 다뤘던 내용이다. "Markov하다" 라는 것은 다음 상태는 과거 상태에는 독립적이고 현재 상태에만 종속을 한다는 것이다. 즉 다음과 같다.

예시로 설명하면 다음과 같다. 현재 내가 장기(체스)를 두고 있다고 하자. 그러면 지금 현재 기물들이 어떻게 놓여져 있는지가 다음 수를 두는 것에 영향을 줄 뿐, 이전에 어떻게 움직였는지는 전혀 다음 수에 도움이 되지 않는다.

State Transition Matrix

Markov를 설명하기 위해 도움이 되는 정의 중 하나이다. state transition probability는 Markov한 state s에서 다음 상태 s'으로 이동할 확률을 뜻하고, Matrix는 이러한 확률을 행렬꼴로 모아둔 것이다.

Markov Process

앞으로 다룰 Markov 대한 성질들의 가장 기본이 되는 과정이다. memoryless random process라고 하는데, 이는 Markov의 특징을 말하는 것이다. Markov Process는 <S,P>로 정의되고, S는 state들의 집합, P는 state transition probability matrix이다. 다음은 아기가 잠에 드는 과정을 도식화한 것이다.

여기서 각 행동은 다 타원형으로 표시되어 있고, '잔다' 라는 상태만 네모로 표시되어 있는데 이는 terminate state, 종료 상태를 의미한다. 각 행동으로 이동하는 화살표에 확률이 써져 있는데, 아직은 모든 상태는 확률에 의해서만 바뀐다. 즉, '눕는다.' 라는 상태에서는 70% 확률로 논다. 라는 상태로 이동하고, 30%으로 확률로 잠에 들기 시작하는 상태로 이동하는 것이다.

상태를 이동하는 상황이 여러가지 있는데 이들을 episodes라고 부른다.

Markov Reward Process

Markov Process에 Reward function이 추가된 개념으로 <S,P,R,r>와 같으며 R은 reward function으로 R_s=E[R_t+1|S_t=s]이고, r 은 감쇠인자로써, 0과 1 사이의 값을 가진다. 이 단계에서 새로 정의되는 개념들이 있어 이를 정리하고 진행한다.

Return

return Gt는 t 시간이 지난 뒤에 얻은 총 보상을 의미한다. 

• Why discount? 감쇠인자를 사용하는 이유는 무엇일까?
  • 수학적으로 편리하다. 감쇠 인자를 0과 1 사이의 값으로 설정을 했기 때문에 return 값이 무한히 커지는 것을 막을 수 있다. 즉 bounded하게 만들 수 있다.
  • 사람이 선호하기 때문이다.
    • 만약 누군가 당신에게 지금 커피를 사줄지? 아님 10달 뒤에 커피를 사줄지 물어볼 수 있다.
      • 대부분 지금 사달라고 할 것이다.
  • 불확실성을 표현하기 위해서
    • 위의 예시로 생각하보면 지금 사달라고 선택을 하는 이유가 10달 뒤에 진짜 커피를 사줄지는 불확실했기 때문일 것이다.

Value Function

value function은 현재 상태 s로 부터 시작했을 때 return의 기댓값을 의미한다.

지금까지 예시에서 감쇠인자 값을 0이라 가정했을 때, 다음과 같이 value function 값이 구해진다.

지금은 state들이 단순해서 충분히 손으로도 계산을 할 수 있지만 더 많은 state들이 복잡하게 연결된다면 손으로 하는 것은 어렵게 될 것이다. 따라서 이를 위해 Bellman Equation이라는 것을 사용한다.

Bellman Equation

value function을 다음과 같이 표현할 수 있다.

Bellman Equation으로 value function을 그림으로 표현하면 다음과 같다. 현재 상태의 value function은 현재 보상을 받은 뒤(Rs)에 다음 상태들의 value function 합(sigma Pss'v(s'))에 감쇠 인자를 곱한 값을 얻는다는 것이다.

 따라서 이와 같이 value function으로만 구성된 식을 matrix form으로 변환한다면 역행렬을 통해서 한번에 구할 수 있게 된다.

하지만 이 연산은 O(n^3)에 해당하는 복잡도를 가지고 있다. 따라서 작은 MRP에서만 계산이 가능하고, 큰 경우는 DP, Monte-Carlo 방법등으로 구하게 된다.

Markov Decision Process

Markov Reward Process에서 action이 추가된 단계이다. <S,A,P,R,r>와 같이 정의 하며 A는 action들의 집합을 의미한다.

또한 action이 추가되었기 때문에 상태천이행렬 P와, reward function R에 a에 관한 식이 들어가게 되었다. 따라서 슬라이드에서 소개한 내용에 action을 추가하면 다음과 같다.

그리고 Action이 생김에 따라서 몇 가지 용어를 정의해야 한다.

Policy

정책 π 는 현재 주어진 상태에서 action a를 수행할 분포를 의미한다.

따라서 정책은 agent 행동을 정의한다고 할 수 있다. 그리고 이 정책을 이용해서 상태천이행렬 P와 reward function R을 다음과 같이 다시 정의할 수 있다.

Value Function

• state-value function

state value function은 현재 상태 s가 주어졌고, 정책을 따른다고 했을 때 얻을 수 있는 return의 기댓값을 의미한다.

• action-value function

action value function은 현재 상태가 s이고, action a를 한다. 그리고 정책을 따른다고 했을 때, 얻을 수 있는 return의 기댓값을 의미한다.

Bellman Expectation Equation

위에서 정의했던 state value function과 action value function을 Bellman equation을 사용하기 위해서 Immediate reward와 future reward 형태로 분해할 수 있게 된다.

하지만 위 식으로는 실제로 구현을 하는 것이 힘들기 때문에 직접 구현을 위해 조금 더 명백한 형태로 변형이 필요하게 됩니다.

 위 그림에서 흰색 원은 state를 의미하고, 검은색 원은 action을 의미합니다. 위 그림을 해석해 보면 현재 상태 s에서 가능한 action들은 2개가 있는 것입니다.(실제로는 더 많은 검은색 점이 있을 수 있습니다.) 그러면 agent가 선택한 당시의 정책에 따라 action을 할 확률이 정해질 것이고, 그 때마다 action-value function을 구할 수 있게 됩니다. 

 따라서 위 그림으로 보아 우리는 현재 state s에서의 state value function을 구하기 위해서 각 action을 할 확률(정책)과 그 action에서 발생하는 value state function을 곱한 것들의 합으로 표현을 할 수 있게 됩니다.

즉 다음과 같이 식을 얻을 수 있습니다.

하지만 아직 이 형태로는 현재 state value function과 다음 state value function과의 관계를 알 수 없습니다. 그러므로 action value function에 대해서 식을 전개해보도록 하겠습니다.

state s에서 action a를 했을 때의 그 action에 대한 value는 두 가지로 나뉘게 됩니다. state s에서 action a를 했을 때의 reward와 그 다음 state의 value function입니다. 그런데 이 중 다음 state value function은 다음 시점의 value function이므로 감쇠 인자를 적용시켜줘야 합니다. 또한 상태가 변한 것이므로 상태 전이 확률도 적용시켜줘야 합니다. 따라서 다음과 같이 식을 구성할 수 있습니다.

따라서 위 두 내용을 모두 한 번에 합치면 다음과 같이 됩니다.

지금까지 state value function을 설명하기 위해 전개를 한 것처럼 이를 action value function을 설명하기 위해 전개를 진행하면 다음과 같이 됨을 알 수 있습니다.

이제 식을 state, action value function 하나씩으로만 표현을 할 수 있기 때문에 이전에 matrix form으로 변경해서 구했떤 것처럼 구할 수 있게 된다.

Bellman Optimal Equation

강화학습은 기본적으로 최대의 보상을 얻는 정책을 찾는 것을 목표로 하고 있기 때문에 얻을 수 있는 기댓값보다는 최대 보상을 얻을 수 있는 것이 더 중요합니다. 따라서 앞서 정의했던 value function들을 다음과 같이 정의할 수 있습니다.

위의 식으로 optimal한 value function을 구할 수 있다면 주어진 state에서 value가 가장 높은 action을 선택할 수 있고, 이를 통해서 optimal한 정책을 구할 수 있게 됩니다. optimal한 값을 항상 얻도록 만들어야 하므로 다음과 같이 정책을 수식을 적을 수 있습니다.

앞서 Expectation Equation에서 진행했던 것처럼 Optimal도 진행을 할 수 있고 다음과 같이 얻을 수 있다.

하지만 Bellman Optimality Equation은 max 연산때문에 non-linear하다. 그렇기 때문에 일반화된 해법을 제공할 수는 없고, 이를 위한 여러가지 다른 방법들을 제시한다.

• Value Iteration
• Policy Iteration
• Q-learning
• Sarsa

강화학습으로 가장 유명한 알파고가 있으며 알파고를 만든 회사인 deepmind에서 David Silver가 강화학습에 대해 강의한 자료를 제공하고 있다. 따라서 이 강의를 보면서 정리한 내용들을 앞으로 올려보도록 한다.

https://www.youtube.com/watch?v=2pWv7GOvuf0&list=PLqYmG7hTraZDM-OYHWgPebj2MfCFzFObQ