아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
3.1 선형 기저 함수 모델
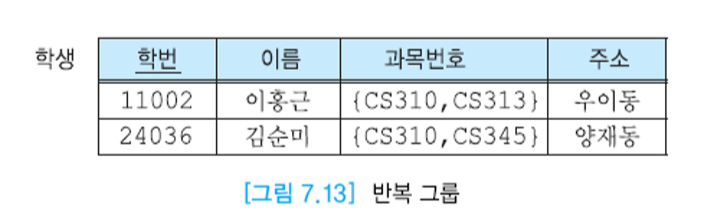
가장 단순한 형태의 선형 회귀 모델은 입력 변수들의 선형 결합을 바탕으로 한 모델
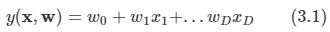
- 여기서 x=(x1,..,xD)T이고, 이 때의 식을 선형 회귀라고 부른다.
한계점을 극복하기 위해서 다음처럼 입력 변수에 대한 고정 비선형 함수들의 선형 결합을 사용할 수 있다.

여기서 함수 파이가 추가된 형태가 되었는데, 이 함수를 기저함수라고 부른다.
w0는 bias라고 부른다. 표기의 편리성을 위해 ϕ0(x)=1 로 정의하면 더 간략한 식으로 기술하기도 한다.

비선형 기저 함수들을 사용했기 때문에 y(x,w)가 입력 벡터 x에 대한 비선형 함수가 되도록 할 수 있다.
- 그럼에도 선형 모델이라고 불리는 이유는 이 함수들이 w에 대해서 선형 함수이기 때문
1장에서 살펴 보았던 다항 회귀 문제에 대해서 다시 알아 보자.
- 입력 변수는 단일 변수 x고, 출력 값인 t도 1차원 실수 값이다.
- 기저 함수를 사용하며 거듭제곱 형태를 가진다.
- 하지만 이 함수는 약간 문제가 있다.
- 입력 변수에 대한 전역적인 함수이기 때문에 입력 공간의 한 영역에서 발생한 변화가 다른 영역들에까지 영향을 미친다는 것이다.
- 이러한 경우 함수 근사를 할 때 문제가 발생하도록 한다.
- 이를 해결하기 위해 입력 공간을 여러 영역들로 나누고 각 영역에 대해서 서로 다른 다항식을 피팅한다. 그리고 이를 스플라인 함수라고 부른다.
- 하지만 이 함수는 약간 문제가 있다.
다양한 다른 함수들이 기저 함수로 사용될 수 있다.

- 가우시안 기저 함수라고 부르며 정규화 계수가 없는데 이는 wj가 존재하기 때문에 생략한 것이다.

시그모이드 형태의 기저 함수다.
- tanh 함수의 선형 결합으로 표현 가능하다.
- 이번 장에서는 어떤 기저 함수를 사용하는지와는 무관하다. 따라서 간략히 소개만 하고 넘어간다.
3.1.1 최대 가능도와 최소 제곱
- 이미 1장에서 최소 제곱법을 사용해서 커브 피팅을 시도했으며 가우시안 노이즈 모델을 가정했을 때 오류 함수를 최소화하는 것이 최대 가능도를 구하는 것에 해당한다는 것도 증명했다.
이를 조금 더 자세히 알아본다. 가우시안 노이즈가 포함된 타겟 t에 대한 함수를 표현해 보자.

여기서 입실론은 0을 평균으로 B를 정밀도로 가지는 가우시안 확률 변수다. 따라서 다음과 같이 적을 수 있다.

위의 식은 주어진 입력 데이터 x에 따른 t에 대한 확률 분포라고 생각하면 된다.
- 확률 분포는 가우시안 분포일 것이다.
가우시안 조건부 분포의 조건부 평균은 다음과 같다.

- 입력 데이터 집합 X={x1,...,xN}과 그에 해당하는 t=t1,...,tN을 고려해 보자.
각각의 데이터가 발현될 가능성은 모두 독립적이라고 가정한다.(i.i.d)
따라서 샘플 데이터를 얻는 확률은 다음과 같이 기술할 수 있다.

x는 언제나 조건부 변수의 집합에 포함되어 있을 것이므로 x를 뺄 수 있다.
로그 함수를 도입하여 수식을 더 간단히 만든다.
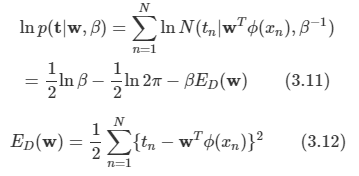
이제 여기에 최대 가능도 방법을 적용하여 w와 B를 구할 수 있다.
w를 구하기 위해 ED(w)를 최소화 하자.

w에 대해 미분하면 위와 같고 좌변을 0으로 두고 전개하면 다음과 같은 식을 얻을 수 있다

이러한 방법을 normal equation이라고 부른다.
- 파라미터의 추정 방식이 업데이트 방식이 아닌 일반 방정식으로 풀이되는 방식이다.
여기서 파이는 design matrix라고 부르며 다음과 같이 생겼다.
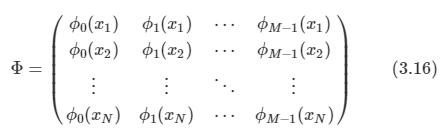
이를 Moor - Penrose pseudo inverse라고도 한다.
- w0에 대해 더 알아보도록 하자.
편향 매개변수를 명시화하면 다음과 같이 적을 수 있다.
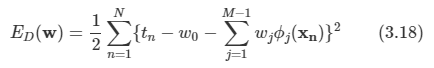
w0에 대한 미분값을 0으로 놓고 w0에 대해 풀면 다음을 구할 수 있다.

w0 값의 의미를 알아 보자.
- 훈련 집합의 타깃 변수들의 평균과 기저 함숫값 평균들의 가중 합 사이의 차이를 보상한다는 것을 알 수 있다.
로그 가능도 함수를 노이즈 정밀도 매개변수 B에 대해 최대화 하게 되면 다음을 얻게 된다.
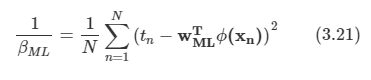
3.1.3. 순차적 학습
- 지금까지 살펴본 MLE 기법은 전체 데이터를 한번에 사용해서 처리하는 배치 방식이다.
- 하지만 큰 데이터 집합에 대해서는 이러한 방식이 계산적으로 실행하기에는 복잡하다.
따라서 큰 데이터 집합에 대해서는 순차적 알고리즘을 사용하는 것이 유용할 수 있다.
- 이를 online 방식이라고도 부른다.
- 한 번에 하나의 데이터 포인트를 고려하며 모델의 매개변수들은 그때마다 업데이트된다.
- 여기서는 확률적 경사 하강법/슨치작 경사 하강법을 적용하여 구현하도록 한다.
여러 데이터 포인트들에 대한 오류 함수의 값이 데이터 포인트 각각의 오류 함수의 값을 합한 것과 같다면 매개변수 벡터 w를 다음과 같이 업데이트할 수 있다.

- 여기서 타우는 반복수를 의미하며, η는 학습률 파라미터이다.
- 위와 같은 알고리즘을 최소 제곱 평균 (LMS)라고 부른다.
3.1.4 정규화된 최소 제곱법
- 정규화는 오버피팅을 방지하기 위해 사용되는 방법이다.
에러 함수는 다음의 형태를 띠게 된다.
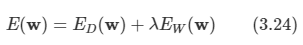
여기서 람다는 정칙화 계수로서 ED(w) 와 EW(w) 사이의 가중치를 조절하게 된다.
식을 정리하면 다음과 같다.
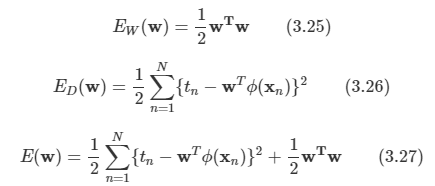
해당 형태의 정규화항은 가중치 감쇠(weight decay)라고 불린다.
- 순차 학습에서 데이터에 의해 지지되지 않는 한 가중치의 값이 0을 향해 감소하기 때문에 이렇게 부르는 것이다.
- 매개변수 축소 방법의 한 예시다.
에러 함수가 w의 이차 함수의 형태로 유지되므로 최소화하는 값을 닫힌 형태로 찾아낼 수가 있다.
최종적으로 식을 정리하면 다음과 같다.

일반적인 형태의 정규화항을 사용하기도 하는데 이 경우 정규화 오류 함수는 다음 형태를 띤다.
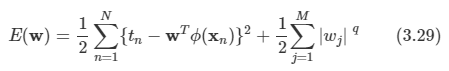
- q=2인 경우 이차 정규화항에 해당하게 된다.
q=1인 경우를 일컬어 라쏘라 한다. 라쏘 정규화를 시행할 경우 람다의 값을 충분히 크게 설정하면
몇몇 개수가 wj가 0이 된다. 이런 모델을 sparse(희박한) 모델이라고 한다.

아래 그림에 대해 유심히 살펴보도록 하자.
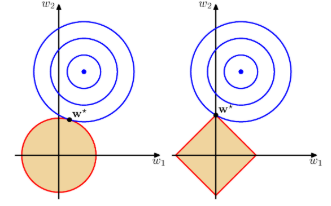
- 왼쪽은 q=2인 경우이고, 오른쪽은 q=1인 경우를 의미한다.
- 사용하는 파라미터는 w0, w1 뿐인 아주 간단한 모델이다.
- 파란 원의 중심이 E(w)를 최소로 만드는 w 벡터 값을 표현한 것이다.
- 정칙화 요소가 없는 경우 이 값을 모델의 파라미터로 사용한다.
- 정칙화 요소가 추가되면 노란색 영역에서만 w 값을 취할 수 있다.
3.1.5 다중 출력값
- 지금까지 출력값 t가 단일 차원의 실수값이었지만 이를 벡터로 확장하여 기술한다.
t 벡터의 크기가 K라고 할 때 각 값은 서로 영향을 주지 않는다.

Likelihood 함수를 정의해보자.
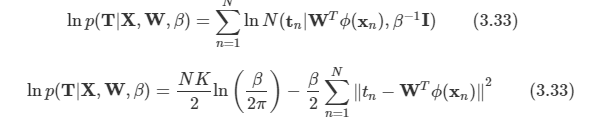
W에 대해 최대화를 할 수 있다.

- 식 자체로의 변화는 없고, 스칼라 변수가 벡터로 확장되었다는 정도이다.
3.2 Bias-Variance 분해
- 지금까지는 회귀 선형 모델을 논의할 때 기저 함수들의 형태와 종류가 둘 다 고정되어 있다고 가정하였다.
- 최소 제곱법을 사용해서 문제를 풀었지만 과적합 문제가 발생할 수 있다.
- 과적합을 해결하기 위해 기저 함수의 수를 제한하면 모델의 유연성에 제약을 가하게 된다.
- 정규항을 사용하면 과적합 문제를 조절하는 것이 가능하다.
- 정규화 계수 λ 값을 적절히 정해야 한다.
- 과적합 문제는 최대 가능도 방법을 사용할 경우에 발생하며 베이지안 방법론을 사용하면 해결가능하다.
- 따라서 베이지안 관점에서 모델 복잡도를 살펴보도록 한다.
- 우선 빈도주의적 관점의 모델 복잡도에 대해 알아보고 이를 편향-분산 트레이드 오프(bias-variance trade-off)라 한다.
1.5.5절에서 회귀 문제의 결정 이론에 대해 논의할 때 오류 함수를 보았다. 따라서 다음과 같은 식을 얻을 수 있다.

결정 이론에서 사용했던 제곱 오류 함수와 모델 매개변수의 최대 가능도 추정치에 해당하는 제곱합 오류 함수는 다르다.

두번째 항은 y(x)와는 직접적인 관련이 없으므로 이 영역은 데이터 노이즈를 의미하게 된다.
첫번째 항은 y(x)로 어떤 것을 선택하느냐에 따라 결정된다.
- 제곱항이기 때문에 항상 0보다 크거나 같다. 그러므로 h(x)와 동일한 y(x)를 찾아야 한다.
- 데이터가 충분히 많다면 충분히 근사된 y(x)를 쉽게 찾을 수 있다.
- 하지만 우리에게는 유한한 숫자 N개의 데이터 포인트들만을 가지고 있다.
이제 몇 가지 가정을 해보자.
- 분포 p(t,x)를 통해 생성된 N개의 샘플로 구성된 데이터 집합 D를 얻을 수 있다.
- 또한 여러 개의 데이터 집합을 얻을 수 있으며 모든 샘플은 서로 독립적으로 생성된다고 가정할 수 있다. (i.i.d)
- 우리는 각 데이터 집합을 사용해 예측함수 y(x;D)를 만들 수 있다.
- 이를 통해 손실 함수와 결과를 얻을 수 있다.

3.37의 첫 번째 항의 피적분 함수는 위와 같은 형태를 띠게 된다. 데이터 집합 D에 대해 종속적이므로 구한 값을 평균을 내어 사용할 수 있다. 괄호 안에 ED[y(x;D)]를 이용해 식을 전개 할 수 있다.

D에 대해 이 식의 기댓값을 구하고 마지막 항을 정리하면 다음과 같이 된다.

- 첫 번째 term을 bias라고 하고, 두 번째 term은 variance라고 한다.
최종적으로 3.37에 식을 대입하면 기대 오류를 다음과 같이 정의할 수 있다.

각각의 값들은 다음과 같다.
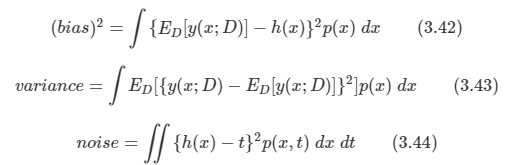
- 우리의 목표는 Expected loss E[L] 값을 최소화하는 것이다. 그리고 이 값은 위의 3가지 요소로 나누어 고려할 수 있다.
편향과 분산 사이에는 trade-off 관계가 있으며 적절히 조절하여 Expected loss가 작도록 해야 한다.
- 아주 유연한 모델은 낮은 bias와 높은 variance
- 엄격한 모델은 높은 bias와 낮은 variance를 가지게 된다.

- 위의 그림은 bias와 variance의 trade-off 관계를 나타낸다.
- L=100개의 데이터 집합들이 있으며, 각각의 집합은 N=25인 데이터 포인트로 구성되어 있다.
- 각각의 학습 결과는 왼쪽 그림의 붉은 색 선이 된다.
- 오른쪽 그림의 붉은 색 그래프는 왼쪽 샘플 집합 결과의 평균 값이며, 녹샌선은 우리가 예측 해야 할 sin2π 곡선이다.
- λ 값을 변화시켜 가면서 결과를 확인한다.
- lnλ값이 큰 경우 높은 bias와 낮은 variance 값을 가진다.
- 따라서 각각의 샘플 집합들 사이의 분산이 작다.
- 실제 예측 범위가 제한적이라 결과가 옳지 않을 수 있다.
- lnλ 값이 작은 경우 낮은 bias와 높은 variance 값을 가진다.
- 예측 값과는 매우 유사한 것을 알 수 있다.
- 하지만 분산도가 매우 크다.
- 샘플 수가 충분하지 못하면 이러한 현상이 발생하기 때문에 샘플 수를 충분히 확보한다.
위와 같은 bias-variance의 trade-off 관계를 수량적으로 확인해 볼 수 있다.
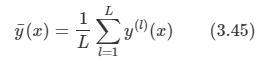
적분된 제곱 bias와 variance에 대한 값은 다음처럼 주어진다.


- 이 그래프를 보면 결국 분홍색 선을 골라야 하는 것을 알 수 있고 이 때 테스트 에러도 최소가 되는 것을 확인할 수 있다.
'Book > Machine Learning' 카테고리의 다른 글
| [ML]ch 4. Linear Models for Classification - part 2 (0) | 2020.02.17 |
|---|---|
| [ML]ch 4. Linear Models for Classification - part 1 (0) | 2020.02.10 |
| [ML]ch 2. Probability Distributions (0) | 2020.01.27 |
| [ML]ch 1. Introduction-part 2 (0) | 2020.01.20 |
| [ML]ch 1. Introduction-part 1 (0) | 2020.01.13 |