아래 모든 내용들은 Christopher Bishop의 pattern recognition and machine learning에서 더 자세히 볼 수 있습니다.
2.3.0 가우시안 분포
-
가우시안 분포는 보통 정규분포로 알려져 있으며 단일 변수 x에 대해 가우시안 분포는 다음과 같이 기술된다.

- 여기서 u는 평균 시그마^2은 분산을 의미하며, 입력 변수가 다차원인 경우에도 기술할 수 있다.
-
가우시안 분포는 단일 실변수에 대해서 엔트로피를 극대화하기 위해 사용된다.
-
또한 여러 확률 변수의 합에 대해 고려하는 경우에 사용되며, 이 때 중심 극한 정리라는 개념을 사용한다.
-
중심 극한 정리
-
표본 평균들이 이루는 분포는 샘플 크기가 큰 경우 모집단의 원래 분포와 상관없이 가우시안 분포를 따르게 된다.
-
즉 동일한 확률 분포를 가지는 N개의 독립 확률 변수들의 평균 값은 N의 크기가 충분히 크다면 가우시안 분포를 따른다는 것이다.
-
표본이 가우시안 분포를 따른다는 것이 아니라 표본의 평균이 가우시안 분포를 따르는 것이다.
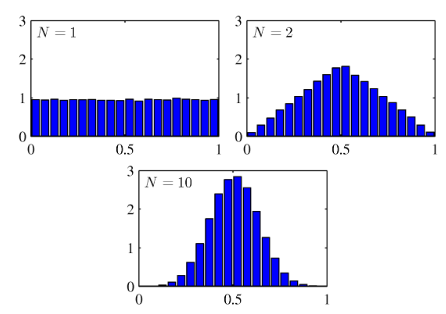
-
N이 커질수록 정규 분포의 모양을 만드는 것을 알 수 있다.
-
-
가우시안 분포의 기하학적인 형태를 살펴보자
-
x에 대한 가우시안 분포의 함수적 종속성은 지수상에서 나타난다.
-
이는 이차식의 형태를 띤다.
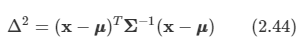
-
여기서의 △ 값은 u로부터 x까지의 마할노비스 거리라고 한다. 이 마할노비스 거리에서 공분산이 항등 행렬이 된다면 유클리디안 거리가 된다.
-
-
지수 연산으로부터 비대칭적인 요소들이 사라질 것이기 때문에 공분산 행렬이 대칭행렬이 된다.
-
따라서 다음과 같은 식을 적용할 수 있다.
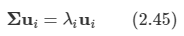
-
공분산 행렬에 대한 모든 고유 벡터는 단위 직교한다. (공분산 행렬이 대칭 행렬이므로)
-
따라서 위에 언급한 ui는 단위 직교 벡터를 의미한다.
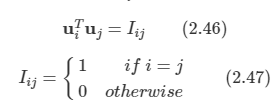
-
-
이제 고유 벡터를 이용해서 공분산 행렬을 전개할 수 있으며 다음의 형태를 띠게 된다.

-
역행렬도 쉽게 구할 수 있다.
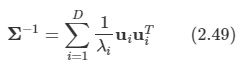
-
이제 이 식을 (2.44)에 대입할 수 있다.
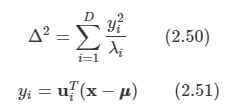
-
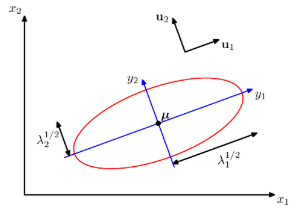
여기서 y는 정규직교 벡터 ui들로 정의되는 새로운 좌표계라고 해석할 수 있다.
- 즉 가우시안 함수의 원점을 u로 옮기고 고유 벡터를 축으로 회전 변환되는 식을 의미한다
-
이러한 변환을 주축 변환이라고 한다.
- 모든 고윳값들이 양의 값을 가진다면 이 표면은 타원형을 띤다.
- 타원형의 중심은 u에 위치하며, 이 타원형의 축은 ui상에 자리하게 된다.
- 각각의 축 방향에 대한 척도 인자는 람다^1/2로 주어진다.
-
y로 정의되는 새로운 좌표 체계상에서의 가우시안 분포의 형태에 대해서 살펴보도록 한다.
-
x 좌표계에서 y 좌표계로 변환되는 과정에서 야코비안 행렬 J를 가지게 된다.
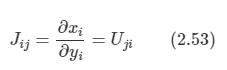
-
여기서 Uji는 행렬 U^T의 원소에 해당한다. U의 정규직교성을 바탕으로 야코비안 행렬의 행렬식 제곱이 다음과 같음을 알 수 있다.
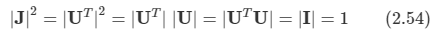
-
공분산 행렬의 행렬식은 고유값의 곱으로 표현할 수 있다.
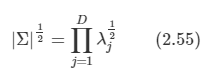
-
-
따라서 yj 좌표계에서 가우시안 분포는 다음의 형태를 가지게 된다

- 이는 D개의 독집적인 단병량 가우시안 분포들의 곱에 해당한다.
- 즉 고유 벡터를 이용해서 축을 변환시켜 얻은 식은 결국 차원간 서로 독립적인 정규 분포를 만들어낸다.
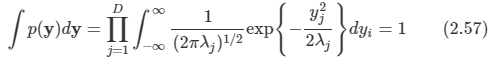
- 역시나 적분 값이 1을 가지는 것을 알 수 있다.
-
가우시안 분포의 모멘트값을 살펴봄으로써 평균과 공분산 행렬을 어떻게 해석할 수 있는지 알아보자.
-
x 축에 대해 평균값을 살펴보는데 z=x-u로 놓고 식을 전개한다.
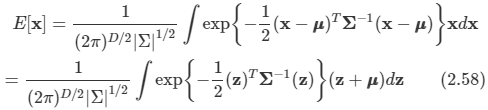
-
이 식은 z에 의해 좌우 대칭인 함수가 만들어진다.
-
z+u가 포함되어 있어서 z 항이 대칭성에 의해 사리게 된다.
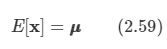
-
다음과 같이 평균이 구해진다.
-
-
이제 2차 모멘트 값을 살펴보도록 한다.
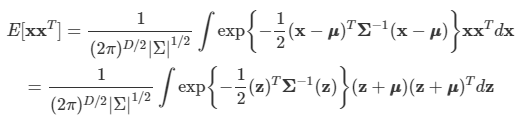
- 여기서 (z+u)(z+u)T를 전개할 수 있으며, 이 수식에서 uzT, zuT는 서로 대칭 관계이므로 제거된다.
- uuT는 수식에서 상수의 역할이므로 적분 바깥 쪽으로 나오게 된다. 정규화 되어 있으므로 1의 값을 가진다.
- zzT 항을 집중해서 보면 된다.
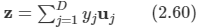
-
여기서 yj= ujTz이다.
-
따라서 식을 다음과 같이 전개 가능하다.
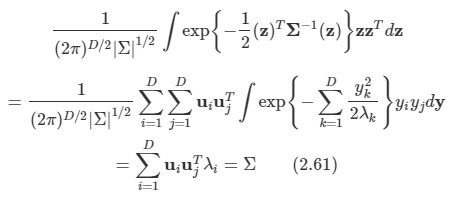
-
원 식에 대입하며 다음과 같은 결과를 얻는다.
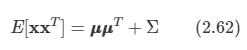
-
공분산 값도 구할 수 있다.
-
E[x]=u이므로 동일한 결과를 얻는다.
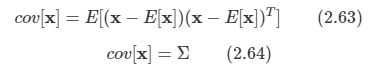
-
-
가우시안 모델은 널리 사용되는 모델이지만 몇 가지 제약들을 가지고 있다.
-
자유 매개변수의 개수
-
D개의 차원을 가진 데이터에서 총 D(D+3)/2 개의 독립적인 파라미터를 가지게 된다.
- u는 D개, 공분산은 D(D+1)/2 개를 가지게 된다.
-
따라서 D가 증가하게 되면 매개변수의 총 개수가 이차로 증가하게 된다.
-
이러한 경우에는 역행렬을 계산하는 것이 매우 느려질 수 있다.
-
이를 해결하는 방법 중 하나는 대각 행렬의 형태를 지닌 공분산 행렬만을 사용한다.
- 이러면 총 2D개의 독립 매개변수만을 고려하면 된다.
- 이에 대응하는 상수 밀도의 경로는 좌표축상에 따라 정렬된 타원의 형태를 띤다.
-
다른 방법은 공분산을 단위행렬에 비례하도록 제한한다.
- 이를 등방성 공분산이라고 부른다.
- D+1개의 독립적인 매개변수가 있다.
- 상수 밀도의 경로가 구의 형태를 띤다.
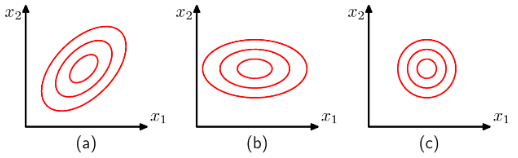
-
(a)는 일반적인 2차원 가우시안 분포, (b)는 공분산이 대각 행렬인 2차원 가우시안 분포, (c)는 공분산이 등방성 공분산인 2차원 가우시안 분포
-
이러한 방법을 통해 자유도를 제한하고 역행렬 계산을 더 빠르게 한다.
-
하지만 확률 밀도의 형태를 상당히 제약시키며, 그에 따라 모델에 데이터상의 흥미로운 상관관계를 표현하는 것을 방해할 수 있다.
-
-
-
분포가 본질적으로 단봉(unimodal) 분포
- 따라서 다봉 분포에 대해 적절한 근사치를 제공할 수 없음.
- 가우시안 분포는 너무 많은 매개변수를 가질 수 있다는 측면에서는 지나치게 유연할 수 있고, 적절하게 표현할 수 있는 분포들의 종류가 제한되어 있다는 측면이 있다.
- 이를 해결하기 위한 방법들
- 잠재변수(latent, hidden, unobserved)를 통해 해결할 수 있다.
- 가우시안 혼합 모델을 통해 해결할 수 있다.
- 계층 모델을 이용하여 이를 해결할 수 도 있다.
- MRF(Markov Random Field)
- 이미지 처리를 위한 확률 모델로 사용
- 픽셀의 공간적 구성을 반영한 구조를 도입해 쉽게 렌더링할 수 있음.
- Linear Dynamaic System
- 시계열 데이터 모델링
- 매우 큰 관측 모델과 잠재 변수의 사용
- 8장에서 이를 다루도록 한다.
- MRF(Markov Random Field)
'Book > Machine Learning' 카테고리의 다른 글
| [ML]ch 4. Linear Models for Classification - part 1 (0) | 2020.02.10 |
|---|---|
| [ML]ch 3. Linear Models for Regression (0) | 2020.02.03 |
| [ML]ch 1. Introduction-part 2 (0) | 2020.01.20 |
| [ML]ch 1. Introduction-part 1 (0) | 2020.01.13 |
| [ML]chapter 0. Beginning (0) | 2020.01.13 |